Question

【题目】已知椭圆 ，过 的直线l与椭圆交于A，B两点，过Q（x0 ， 0）（|x0|＜a）的直线l'与椭圆交于M，N两点．

（1）当l的斜率是k时，用a，b，k表示出|PA||PB|的值；
（2）若直线l，l'的倾斜角互补，是否存在实数x0 ， 使 为定值，若存在，求出该定值及x0 ， 若不存在，说明理由．

Answer 1

【答案】
（1）解：椭圆 ，焦点在x轴上，焦距为2c，

设直线AB的方程： ，

由 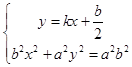，整理得： ，

由韦达定理可知： ，

（2）解：当直线MN的斜率存在时：设直线MN的方程：y=﹣k（x﹣x0），M（x3，y3），N（x4，y4）．

由 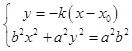，可知得： ，

则 ，

由韦达定理可知： ，

由弦长公式可知：丨MN丨= ，

∴ ，

，

∴当x0=0时， 为常数

当直线MN的斜率不存在时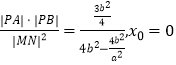： 时，

为定值．

综上：所以当x0=0时， 为常数

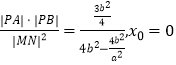【解析】（1）由题意可知：椭圆的焦点在x轴上，设直线AB的方程： ，代入椭圆方程，由韦达定理 ，因此，由弦长公式可知： ，（2）当直线MN的斜率存在时：设直线MN的方程：y=﹣k（x﹣x0），代入椭圆方程，由韦达定理可知： ，由弦长公式求得丨MN丨，则 ， ，当x0=0时， 为常数，当直线MN的斜率不存在时： 时， 为定值，所以当x0=0时， 为常数．