
已知:如图,α∩β=l,a∥α,a∥β.

求证:a∥l.
解析:证明本题可以利用线面平行的性质定理,可用同一法.

证法一:过a作平面γ交平面α于b,
∵a∥α,∴a∥b.同样,过a作平面ξ交平面β于C.
∵a∥β,∴a∥C.∴b∥C.
又∵b![]() β且C
β且C![]() β,∴b∥β.
β,∴b∥β.
又平面α经过b交β于l.
∴b∥l,且a∥b.∴a∥l.
证法二:在l上任取一点A,过A和a作平面和α相交于l1,和β相交于l2.
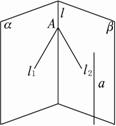
∵a∥α,∴a∥l1.
∵a∥β,∴a∥l2.
但过一点只能作一条直线与另一条直线平行,
∴l1与l2重合.
又∵l1![]() α,l2
α,l2![]() β,
β,
∴l1和l2重合于l.
∴a∥l.
点评:(1)应用线面平行的性质定理时,应着力寻找过已知直线的平面与已知平面的交线,有时为了得到交线还需作出辅助平面.
(2)证法二用到了结论“过空间直线外一点有且只有一条直线和已知直线平行”,且本证法是“同一法”.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com