
(本题满分16分)围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽度为2m的进出口,如图所示已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元)
⑴将y表示为x的函数;
⑵写出f(x)的单调区间,并证明;
⑶根据⑵,试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用。

解:⑴如图,设矩形的另一边长为a m
则y=45x+180(x-2)+180×2a=225x+360a-360
由已知 ax=360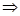 a=
a=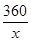
∴y=225x+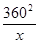 -360(x>0) ……………………………………………6′
-360(x>0) ……………………………………………6′
⑵任取x1>x2>0
y1-y2=225(x1-x2)+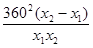
=(x1-x2)(
225- ) ……………………………………10′
) ……………………………………10′
∴x1x2>(
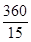 )2=242时, y1>y2
)2=242时, y1>y2
x1x2<24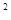 时, y1
时, y1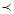 y2
y2

∴x1>x2≥24时
y1>y2 24> x1>x2>0时
y1<y2
即f(x)在(0,24)单调减,在(24,+∞)单调增 …………………14′
⑶x=24时,修建围墙的总费用最小,最小费用为10440元…………………16
【解析】略


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2014届江苏省高二上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分16分)已知直线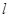 :
:
(1)求证:不论实数 取何值,直线
取何值,直线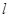 总经过一定点.
总经过一定点.
(2)为使直线不经过第二象限,求实数 的取值范围.
的取值范围.
(3)若直线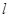 与两坐标轴的正半轴围成的三角形面积最小,求
与两坐标轴的正半轴围成的三角形面积最小,求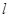 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2013届江苏南通第三中学高二下学期期中考试文科数学试卷(解析版) 题型:解答题
本题满分16分)
设函数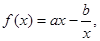 曲线
曲线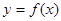 在点
在点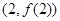 处的切线方程为
处的切线方程为 .
.
(1)求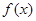 的解析式;
的解析式;
(2)证明:曲线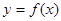 上任一点处的切线与直线
上任一点处的切线与直线 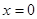 及直线
及直线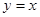 所围成的三角形的面积是一个定值,并求此定值.
所围成的三角形的面积是一个定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
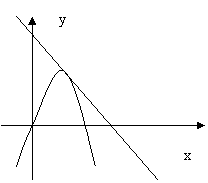 (本题满分16分)开口向下的抛物线
(本题满分16分)开口向下的抛物线![]() 在第一象限内与直线
在第一象限内与直线![]() 相切.此抛物线与
相切.此抛物线与![]() 轴所围成的图形的面积记为
轴所围成的图形的面积记为![]() .
.
(1)求![]() 与
与![]() 的关系式,并用
的关系式,并用![]() 表示
表示![]() 的表达式;
的表达式;
(2)求使![]() 达到最大值的
达到最大值的![]() 、
、![]() 值,并求
值,并求![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
 (本题满分16分)开口向下的抛物线
(本题满分16分)开口向下的抛物线![]() 在第一象限内与直线
在第一象限内与直线![]() 相切.此抛物线与
相切.此抛物线与![]() 轴所围成的图形的面积记为
轴所围成的图形的面积记为![]() .
.
(1)求![]() 与
与![]() 的关系式,并用
的关系式,并用![]() 表示
表示![]() 的表达式;
的表达式;
(2)求使![]() 达到最大值的
达到最大值的![]() 、
、![]() 值,并求
值,并求![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com