����⣺��1����Q
n��x
n��y
n����Q
n+1��x
n+1��y
n+1����
���P
n��������x
n��y
n+1��
��
Q1(1��1)��P(1��) ��Q2(��)��-----------------------------------��2�֣�
��2����Q
n��Q
n+1������C�ϣ�
��
yn=��
yn+1=��
�֡�P
n������C
n�ϣ�
��
yn+1=��--------------------------------��4�֣�
��x
n+1=x
n+2
-n��
��a
n=2
-n��-----------------------------------------��6�֣�
��3��x
n=��x
n-x
n-1��+��x
n-1-x
n-2��+��+��x
2-x
1��+x
1=2
-��n-1��+2
-��n-2��+��+2
-1+1
=
1-=2-2
1-n��-------------------��9�֣�
��a
n•b
n=��x
n+1-x
n��•��y
n-y
n+1��
=
2-n(-)=
(-)=
��
��2•2
n-2��2
n��2•2
n-1��3��
��
an•bn����--------------------------------��12�֣�
��S
n=a
1b
1+a
2b
2+��+a
nb
n��++��+=•=(1-)��-----------------------��14�֣�

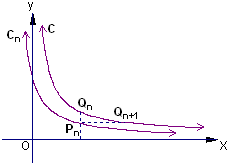 ��ͼ����֪����C��y=
��ͼ����֪����C��y=

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
 ��ͼ����֪����C��y=
��ͼ����֪����C��y=
 ��ͼ����֪����C��y=
��ͼ����֪����C��y= ��2006•�Ͼ���ģ����ͼ����֪����C��y=
��2006•�Ͼ���ģ����ͼ����֪����C��y= ��ͼ����֪����C��y=x2��0��x��1����O��0��0����Q��1��0����R��1��1����ȡ�߶�OQ���е�A1����A1��x��Ĵ��߽�����C��P1����P1��y��Ĵ��߽�RQ��B1����a1Ϊ����A1P1B1Q��������ֱ�ȡ�߶�OA1��P1B1���е�A2��A3����A2��A3�ֱ���x��Ĵ��߽�����C��P2��P3����P2��P3�ֱ���y ��Ĵ��߽�A1P1��RB1��B2��B3����a2Ϊ��������A2P2B2A1�����A3P3B3B1�����֮�ͣ��Դ����ƣ���anΪ2n-1���������֮�ͣ��Ӷ�������{an}����������е�ǰn���ΪSn��
��ͼ����֪����C��y=x2��0��x��1����O��0��0����Q��1��0����R��1��1����ȡ�߶�OQ���е�A1����A1��x��Ĵ��߽�����C��P1����P1��y��Ĵ��߽�RQ��B1����a1Ϊ����A1P1B1Q��������ֱ�ȡ�߶�OA1��P1B1���е�A2��A3����A2��A3�ֱ���x��Ĵ��߽�����C��P2��P3����P2��P3�ֱ���y ��Ĵ��߽�A1P1��RB1��B2��B3����a2Ϊ��������A2P2B2A1�����A3P3B3B1�����֮�ͣ��Դ����ƣ���anΪ2n-1���������֮�ͣ��Ӷ�������{an}����������е�ǰn���ΪSn��