
分析 (1)直接利用奇函数的定义,化简即可求m的值
(2)利用loga$\frac{1+x}{1-x}$>0,$\left\{\begin{array}{l}{\frac{1+x}{1-x}>0}\\{\frac{1+x}{1-x}>1}\end{array}\right.$即可
(3)构造u=$\frac{1+x}{1-x}$=$\frac{2}{1-x}$-1,判断单调性,再利用复合函数单调性证明即可.
解答 解:(1)∵f(x)是奇函数,∴f(-x)=-f(x),即-loga$\frac{1+mx}{1-x}$=loga$\frac{1-mx}{1+x}$
得m=1
(2)f(x)=loga$\frac{1+x}{1-x}$
∴loga$\frac{1+x}{1-x}$>0
$\left\{\begin{array}{l}{\frac{1+x}{1-x}>0}\\{\frac{1+x}{1-x}>1}\end{array}\right.$即0<x<1
故不等式f(x)>0的解集;:{x|0<x<1}
(3)a=2,f(x)=log2$\frac{1+x}{1-x}$,定义域为(-1,1)单调递增
∵u=$\frac{1+x}{1-x}$=$\frac{2}{1-x}$-1,设任意两个实数x1,x2,-1<x1<x2<1
u(x2)=$\frac{2}{1-{x}_{2}}$-1,u(x1)=$\frac{2}{1-{x}_{1}}$-1
∴u(x2)-u(x1)=$\frac{2}{1-{x}_{1}}$-1-$\frac{2}{1-{x}_{2}}$+1=$\frac{2({x}_{1}-{x}_{2})}{(1-{x}_{1})(1-{x}_{2})}$
∵-1<x1<x2<1,
∴x1-x2<0,1-x1>0,1-x2>0
∴u(x2)-u(x1)<0
u(x2)<u(x1)
即log2u(x2)<log2u(x1)
即(-1,1)单调递增
点评 本题综合考察了函数的定义,单调性的定义,运用解析式判断证明,关键是恒等变形能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCB′,△ABC≌△AB′C,AB⊥AB′,cos∠BCB′=$\frac{3}{4}$,BC=2$\sqrt{2}$.
如图,在四边形ABCB′,△ABC≌△AB′C,AB⊥AB′,cos∠BCB′=$\frac{3}{4}$,BC=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}+1}}{2}$ | B. | $\sqrt{3}+1$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\sqrt{5}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
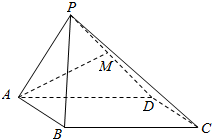 如图,四棱锥P-ABCD中,侧面PAD⊥底面ABCD,其中,四边形ABCD为正方形,△PAD是正三角形,M是PD的中点.
如图,四棱锥P-ABCD中,侧面PAD⊥底面ABCD,其中,四边形ABCD为正方形,△PAD是正三角形,M是PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com