
分析 (Ⅰ)因为P={x|-1<x<2},所以方程mx2-(3m+1)x+2(m+1)=0的两根为-1和2,根据根与系数的关系即可求出m的值;
(Ⅱ)不等式mx2-(3x+1)x+2(2m+1)>0可化为(x-2)[mx-(m+1)]>0,需要分类讨论,即得到不等式的解集;
(Ⅲ)依题意,当x∈(-3,2)时,不等式mx2-(3m+1)x+2(m+1)>0恒成立,分类讨论即可求出m的范围.
解答 解:(I)因为P={x|-1<x<2},
所以方程mx2-(3m+1)x+2(m+1)=0的两根为-1和2.
将x=-1代入上述方程,得m(-1)2-(3m+1)(-1)+2(m+1)=0,
解得m=$-\frac{1}{2}$.
(II)不等式mx2-(3x+1)x+2(2m+1)>0可化为(x-2)[mx-(m+1)]>0.
当m>0时,方程m(-1)2-(3m+1)(-1)+2(m+1)=0的两根为$\frac{m+1}{2}$和2.
①当$\frac{m+1}{m}$=2,即m=1时,解得x≠2.
②当$\frac{m+1}{m}$>2,即0<m<1时,解得x<2或x>$\frac{m+1}{m}$.
③当$\frac{m+1}{m}$<2,即m>1时,解得x<$\frac{m+1}{m}$或x>2.
综上,当0<m<1时,P={x|x<2或x>$\frac{m+1}{m}$};当m=1时,P={x|x∈R,且x≠2};当m>1时,P={x|x<$\frac{m+1}{m}$或x>2}.
(III)依题意,当x∈(-3,2)时,不等式mx2-(3m+1)x+2(m+1)>0恒成立.
当m=0时,原不等式化为-x+2>0,即P={x|x<2},适合题意.
当m>0时,由(II)可得0<m≤1时,适合题意.
当m<0时,因为$\frac{m+1}{m}$=1+$\frac{1}{m}<2$,所以P={x|$\frac{m+1}{m}$<x<2}.
此时必有$\frac{m+1}{m}$≤-3成立,解得$-\frac{1}{4}≤m<0$.
综上,若{x|-3<x<2}⊆P,则m的取值范围是[$-\frac{1}{4},1$].
点评 本题考查了一元二次不等式的解法,分类讨论是关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
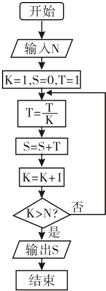
| A. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ | B. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$ | ||
| C. | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$+$\frac{1}{5}$ | D. | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$+ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(2) | B. | (2)(4) | C. | (1)(4) | D. | (1)(2)(3)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com