
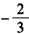 ,
,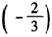 =-2,
=-2,

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| ab |
查看答案和解析>>
科目:高中数学 来源:北京市海淀区2012届高三下学期期中练习数学文科试题 题型:022
已知函数f(x)=![]() 则f(f(x))=________;
则f(f(x))=________;
下面三个命题中,所有真命题的序号是________.
①函数f(x)是偶函数;
②任取一个不为零的有理数T,f(x+T)=f(x)对x∈R恒成立;
③存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3))使得△ABC为等边三角形.
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试、理科数学(上海卷) 题型:044
若实数x、y、m满足|x-m|>|y-m|,则称x比y远离m.
(1)若x2-1比1远离0,求x的取值范围;
(2)对任意两个不相等的正数a、b,证明:a3+b3比a2b+ab2远离2ab![]() ;
;
(3)已知函数f(x)的定义域 .任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明).
.任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明).
查看答案和解析>>
科目:高中数学 来源:2010年全国普通高等学校招生统一考试、文科数学(上海卷) 题型:044
若实数x、y、m满足|x-m|<|y-m|,则称x比y接近m.
(1)若x2-1比3接近0,求x的取值范围;
(2)对任意两个不相等的正数a、b,证明:a2b+ab2比a3+b3接近2ab ;
;
(3)已知函数f(x)的定义域D={x|x≠kπ,k∈Z,x∈R}.任取x∈D,f(x)等于1+sinx和1-sinx中接近0的那个值.写出函数f(x)的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
查看答案和解析>>
科目:高中数学 来源:上海高考真题 题型:解答题
 ;
; ,k∈Z,x∈R},任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明).
,k∈Z,x∈R},任取x∈D,f(x)等于sinx和cosx中远离0的那个值.写出函数f(x)的解析式,并指出它的基本性质(结论不要求证明). 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com