
本小题满分10分)设函数 ,
,
(Ⅰ)求函数 的最大值和最小正周期.,
的最大值和最小正周期.,
(Ⅱ)设A,B,C为 ABC的三个内角,若
ABC的三个内角,若 ,且C为锐角,求
,且C为锐角,求
(1)f(x)的最大值为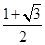 ,最小正周期
,最小正周期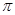 .
.
(2)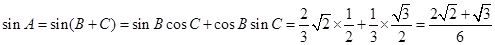
【解析】
试题分析:(1)首先利用二倍角公式化为单一函数,求解最值。
(2)在第一问的基础上,进一步利用同角关系得到B的正弦值和余弦值,然后结合内角和定理,运用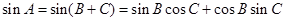 求解得到。
求解得到。
解: (1)f(x)=cos(2x+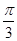 )+sin
)+sin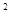 x.=
x.=
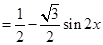 所以函数f(x)的最大值为
所以函数f(x)的最大值为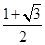 ,最小正周期
,最小正周期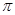 .
.
(2)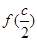 =
=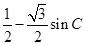 =-
=-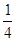 ,
所以
,
所以 , 因为C为锐角, 所以
, 因为C为锐角, 所以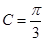 ,
,
又因为在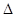 ABC
中, cosB=
ABC
中, cosB=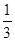 ,
所以
,
所以 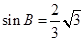 ,
,
所以
考点:本试题主要考查了三角函数的图像与性质的运用。
点评:解决该试题的关键是将函数化为单一函数,结合三角函数的性质得到其最值和周期,统统是结合三角形中同角关系式和两角和差的公式能得到解三角形。


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中数学 来源:2011届贵州省遵义四中7校高三联考理数试题 题型:填空题
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分10分)
设向量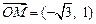 ,向量
,向量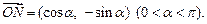
(1)若向量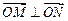 ,求
,求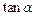 的值;
的值;
(2)求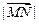 的最大值及此时
的最大值及此时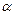 的值。
的值。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年甘肃省高三(奥班)10月月考理科数学试卷(解析版) 题型:解答题
选修4-5:不等式选讲(本小题满分10分)
设函数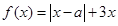 ,其中
,其中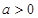 。
。
(Ⅰ)当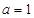 时,求不等式
时,求不等式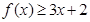 的解集;
的解集;
(Ⅱ)若不等式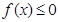 的解集为
的解集为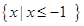 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中数学 来源:浙江省富阳市2009-2010学年度高一数学期中试卷 题型:解答题
(本小题满分10分)设数列 前n项和为
前n项和为 ,且
,且
(1)求 的通项公式;
的通项公式;
(2)若数列 满足
满足 且
且 (n≥1),求数列
(n≥1),求数列 的通项公式
的通项公式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com