
某经销商试销A、B两种商品一个月(30天)的记录如下:
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 2 | 5 | 7 | 7 | 5 | 4 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:高中数学 来源: 题型:解答题
省少年篮球队要从甲、乙两所体校选拔队员。现将这两所体校共20名学生的身高绘制成如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.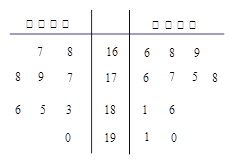
(1)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随
机选2人,那么至少有一人是“高个子”的概率是多少?
(2)从两队的“高个子”中各随机抽取1人,求恰有1人身高达到190cm的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了了解某班的男女生学习体育的情况,按照分层抽样分别抽取了10名男生和5名女生作为样本,他们期末体育成绩的茎叶图如图所示,其中茎为十位数,叶为个位数。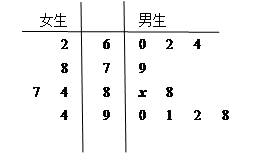
(Ⅰ)若该班男女生平均分数相等,求x的值;
(Ⅱ)若规定85分以上为优秀,在该10名男生中随机抽取2名,优秀的人数记为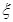 ,求
,求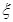 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数 及天数如下表:
及天数如下表:
售出个数 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,得到如下数据:
(Ⅰ)若用表中数据所得频率代替概率,则处罚10元时与处罚20元时,行人会闯红灯的概率的差是多少?
(Ⅱ)若从这5种处罚金额中随机抽取2种不同的金额进行处罚,在两个路口进行试验.
求这两种金额之和不低于20元的概率;
②若用X表示这两种金额之和,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校50名学生参加智力答题活动,每人回答3个问题,答对题目个数及对应人数统计结果见下表:
| 答对题目个数 | 0 | 1 | 2 | 3 |
| 人数 | 5 | 10 | 20 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人参加普法知识竞赛,共有10道不同的题目,其中选择题6道,判断题4道,甲、乙两人各抽一道(不重复).
(1)甲抽到选择题,乙抽到判断题的概率是多少?
(2)甲、乙二人中至少有一人抽到选择题的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.
(Ⅰ)求第4局甲当裁判的概率;
(Ⅱ)X表示前4局中乙当裁判的次数,求X的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com