
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据导数几何意义得切线斜率为![]() ,再根据点斜式得切线方程(2)根据分母符号转化为:
,再根据点斜式得切线方程(2)根据分母符号转化为: ![]() 时
时![]() ,
, ![]() 时
时![]() ,研究
,研究![]() ,其导函数有两个零点
,其导函数有两个零点![]() 或
或![]() ,根据
,根据![]() 与0,1大小分类讨论,确定函数单调性,进而确定函数最值,解对应不等式可得实数
与0,1大小分类讨论,确定函数单调性,进而确定函数最值,解对应不等式可得实数![]() 的值.
的值.
试题解析:(1)![]() 时,
时, ![]() ,
, ![]() ∴切点为
∴切点为![]()
![]() ,
, ![]() ∴切线方程为
∴切线方程为![]()
即曲线![]() 在
在![]() 处的切线方程
处的切线方程![]()
(2)∵当![]() 且
且![]() 时,不等式
时,不等式![]() 恒成立
恒成立
∴![]() 时
时![]() ∴
∴![]()
又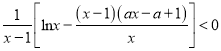 即
即![]() 对
对![]() 且
且![]() 恒成立
恒成立
等价于![]() 时
时![]() ,
, ![]() 时
时![]() 恒成立
恒成立
∵![]()
![]()
令![]() ∵
∵![]() ∴
∴![]() 或
或![]()
①![]() 时,即
时,即![]() 时,
时, ![]() 时,
时, ![]()
∴![]() 在
在![]() 单调递增∴
单调递增∴![]() ,∴
,∴![]() 不符合题意
不符合题意
②当![]() 时,即
时,即![]() 时,
时, ![]() 时
时![]() ∴
∴![]() 在
在![]() 单调递减
单调递减
∴![]() ;
; ![]() 时
时![]() ∴
∴![]() 在
在![]() 单调递减∴
单调递减∴![]()
∴![]() 符合题意
符合题意
③当![]() 时,即
时,即![]() 时,
时, ![]() 时,
时, ![]()
∴![]() 在
在![]() 单调递增∴
单调递增∴![]() ∴
∴![]() 不符合题意
不符合题意
④当![]() 时,即
时,即![]() 时,
时, ![]() 时,
时, ![]() ∴
∴![]() 在
在![]() 单调递增
单调递增
∴![]() ∴
∴![]() 不符合题意
不符合题意
综上, ![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,![]() 为正三角形,且侧面PAB⊥底面ABCD,
为正三角形,且侧面PAB⊥底面ABCD, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 在线段
在线段![]() 上.
上.
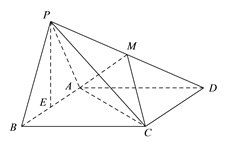
(I)当![]() 是线段
是线段![]() 的中点时,求证:PB // 平面ACM;
的中点时,求证:PB // 平面ACM;
(II)求证: ![]() ;
;
(III)是否存在点![]() ,使二面角
,使二面角![]() 的大小为60°,若存在,求出
的大小为60°,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某市地产数据研究的数据显示,2016年该市新建住宅销售均价走势如下图所示,为抑制房价过快上涨,政府从8月采取宏观调控措施,10月份开始房价得到很好的抑制.
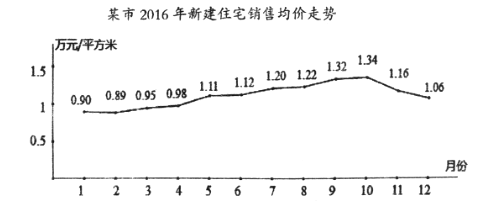
(1)地产数据研究院发现,3月至7月的各月均价![]() (万元/平方米)与月份
(万元/平方米)与月份![]() 之间具有较强的线性相关关系,试建立
之间具有较强的线性相关关系,试建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
(2)地产数据研究院在2016年的12个月份中,随机抽取三个月的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据: ![]() ,
, ![]() ,
, ![]() ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
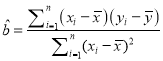 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
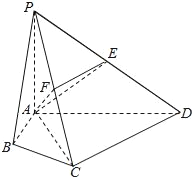
【题目】(14分)在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;
(Ⅲ)求证CE∥平面PAB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com