
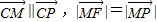 .
.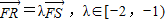 ,求直线l 的纵截距的取值范围.
,求直线l 的纵截距的取值范围.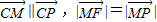 ,可得动点M的轨迹E是以C,F为左、右焦点的椭圆,由此可得轨迹方程;
,可得动点M的轨迹E是以C,F为左、右焦点的椭圆,由此可得轨迹方程;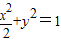 ,利用韦达定理,及
,利用韦达定理,及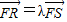 ,即可求得结论.
,即可求得结论.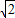
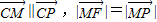
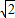
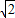 ,c=1
,c=1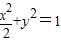 ;
;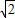 ,0),S(
,0),S(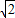 ,0),F(1,0),
,0),F(1,0),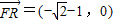 ,
,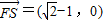
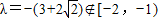 ,故直线l的纵截距不可能为0;
,故直线l的纵截距不可能为0;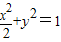 ,可得(t2+2)y2+2ty-1=0
,可得(t2+2)y2+2ty-1=0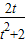 ,y1y2=-
,y1y2=-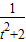
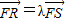 ,∴y1=λy2,∴λ=
,∴y1=λy2,∴λ=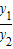 ,λ<0
,λ<0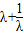 +2=
+2=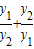 +2=
+2=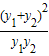 =-
=-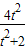
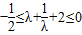
 ≤-
≤-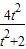 ≤0
≤0
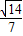 或
或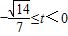
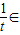
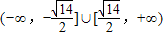 .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
| CM |
| CP |
| MF |
| MP |
| FR |
| FS |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都市高三(上)摸底数学试卷(文科)(解析版) 题型:解答题
 .
.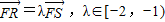 ,求直线l 的纵截距的取值范围.
,求直线l 的纵截距的取值范围.查看答案和解析>>
科目:高中数学 来源:2012年福建省厦门市高三5月适应性考试数学试卷(理科)(解析版) 题型:选择题
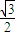
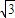
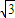
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com