[题目]求满足下列条件的曲线方程(1)已知椭圆以坐标轴为对称轴.且长轴长是短轴长的3倍.点在该椭圆上.求椭圆的方程.(2)已知双曲线的离心率为.焦点是..求双曲线标准方程. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】求满足下列条件的曲线方程

（1）已知椭圆以坐标轴为对称轴，且长轴长是短轴长的3倍，点在该椭圆上，求椭圆的方程.

（2）已知双曲线的离心率为，焦点是，，求双曲线标准方程.

【答案】(1)或；.

【解析】

（1）根据焦点坐标的位置不同，结合题意，分类讨论即可求得；

（2）设出双曲线方程，根据离心率和焦点坐标即可求得.

（1）当椭圆的焦点在轴上时，设椭圆方程为，

由题可知，又因为长轴长是短轴长的3倍，则,

则椭圆方程为：；

当椭圆的焦点在轴上时，设椭圆的方程为，

由题可知，又因为长轴长是短轴长的3倍，则，

则椭圆方程为.

综上所述，椭圆方程为或.

（2）由题可知，双曲线是等轴双曲线，且焦点在轴上，

故可设双曲线方程为，

又因为焦点是，，

故可得，解得，

故双曲线方程为.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

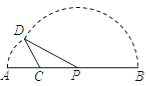
【题目】如图，线段AB=8，点C在线段AB上，且AC=2，P为线段CB上一动点，点A绕着C旋转后与点B绕点P旋转后重合于点D，设CP=x，△CPD的面积为f（x）．求f（x）的最大值（　　）．

A. 　　　 B． 2

C．3 　　　 D．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知抛物线，其焦点到准线的距离为2，直线与抛物线交于，两点，过，分别作抛物线的切线，，与交于点.

（Ⅰ）求的值；

（Ⅱ）若，求面积的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f(x)＝|x＋a|＋|x－2|.

(1)当a＝－3时，求不等式f(x)≥3的解集；

(2)若f(x)≤|x－4|的解集包含[1，2]，求a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】2019年春节期间．当红彩视明星翟天临“不知“知网””学术不端事件在全国闹得沸沸扬扬，引发了网友对亚洲最大电影学府北京电影学院、乃至整个中国学术界高等教育乱象的反思．为进一步端正学风，打击学术造假行为，教育部日前公布的《教育部2019年部门预算》中透露，2019年教育部拟抽检博士学位论文约6000篇，预算为800万元．国务院学位委员会、教育部2014年印发的《博士硕士学位论文抽检办法》通知中规定：每篇抽检的学位论文送3位同行专家进行评议，3位专家中有2位以上（含2位）专家评议意见为“不合格”的学位论文．将认定为“存在问题学位论文”。有且只有1位专家评议意见为“不合格”的学位论文，将再送2位同行专家进行复评．2位复评专家中有1位以上（含1位）专家评议意见为“不合格”的学位论文，将认定为“存在问题学位论文”。设毎篇学位论文被毎位专家评议为“不合格”的槪率均为，且各篇学位论文是否被评议为“不合格”相互独立．