
【题目】(本小题满分13分)设数列![]() 的前
的前![]() 项和为
项和为![]() .已知
.已知![]() ,
, ![]() ,
, ![]() .
.
(1)写出![]() 的值,并求数列
的值,并求数列![]() 的通项公式;
的通项公式;
(2)记![]() 为数列
为数列![]() 的前
的前![]() 项和,求
项和,求![]() ;
;
(3)若数列![]() 满足
满足![]() ,
, ![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】港珠澳大桥于2018年10月24日正式通车,它是中国境内一座连接香港、珠海和澳门的桥隧工程,桥隧全长55千米,桥面为双向六车道高速公路,大桥通行限速100 km/h. 现对大桥某路段上汽车行驶速度进行抽样调查,画出频率分布直方图(如图).根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过90 km/h的概率分别为

A. ![]() ,
,![]() B.
B. ![]() ,
,![]()
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈三中群力校区高二、六班同学用随机抽样的办法对所在校区老师的饮食习惯进行了一次调查, 饮食指数结果用茎叶图表示如图, 图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.

(1)完成下列![]() 列联表:
列联表:

能否有![]() 的把握认为老师的饮食习惯与年龄有关?
的把握认为老师的饮食习惯与年龄有关?
(2)从调查的结果中饮食指数在![]() 的老师内任选3名老师, 设“选到的三位老师饮食指数之和不超过105”为事件
的老师内任选3名老师, 设“选到的三位老师饮食指数之和不超过105”为事件![]() , 求事件
, 求事件![]() 发生的概率;
发生的概率;
(3)为了给食堂提供老师的饮食信息, 根据(1)的结论,能否有更好的抽样方法来估计老师的饮食习惯, 并说明理由.
附:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三复习效果,从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩,分成6组制成频率分布直方图如图所示:
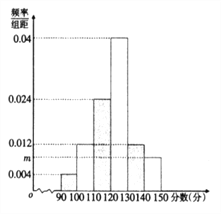
(1)求![]() 的值及这50名同学数学成绩的平均数
的值及这50名同学数学成绩的平均数![]() ;
;
(2)该学校为制定下阶段的复习计划,从成绩在![]() 的同学中选出3位作为代表进行座谈,若已知成在
的同学中选出3位作为代表进行座谈,若已知成在![]() 的同学中男女比例为2:1,求至少有一名女生参加座谈的概率.
的同学中男女比例为2:1,求至少有一名女生参加座谈的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某地区乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号 | 1 | 2 | 3 | 4 | 5 | 6 |
储蓄存款 | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
(1)求关于![]() 的回归方程
的回归方程![]() ,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
(2)在含有一个解释变量的线性模型中,![]() 恰好等于相关系数
恰好等于相关系数![]() 的平方,当
的平方,当![]() 时,认为线性回归模型是有效的,请计算
时,认为线性回归模型是有效的,请计算![]() 并且评价模型的拟合效果(计算结果精确到
并且评价模型的拟合效果(计算结果精确到![]() ).
).
附:
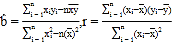 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南京江北新区是第十三个国家级新区,随着新区的经济发展,老城区将不断的进行开发和改造,如图为边长为4km的正三角形![]() 区域,
区域,![]() 分别在三边
分别在三边![]() 上,且
上,且![]() 为
为![]() 的中点,
的中点,![]() ,现将对正三角形
,现将对正三角形![]() 区域进行规划,规划
区域进行规划,规划![]() 区域为娱乐广场,其他区域为生活居住区.
区域为娱乐广场,其他区域为生活居住区.
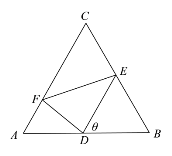
(1)若![]() ,求娱乐广场
,求娱乐广场![]() 的面积;
的面积;
(2)求生活区域的面积![]() 的最大值,并写出
的最大值,并写出![]() 取得最大值时
取得最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:
甲运动员得分:13,51,23,8,26,38,16,33,14,28,39;
乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39.
(1)用十位数为茎,在答题卡中画出原始数据的茎叶图;
(2)用分层抽样的方法在乙运动员得分十位数为 2,3,4 的比赛中抽取一个容量为 5 的样本,从该样本中随机抽取 2 场,求其中恰有 1 场得分大于 40 分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)求证:对![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个交点;
总有两个交点;
(2)设直线![]() 与圆
与圆![]() 交于点
交于点![]() ,若
,若![]() ,直线
,直线![]() 的倾斜角;
的倾斜角;
(3)设直线![]() 与圆
与圆![]() 交于点
交于点![]() ,若定点
,若定点![]() 满足
满足![]() ,求此时直线
,求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】语音交互是人工智能的方向之一,现在市场上流行多种可实现语音交互的智能音箱,它们可以通过语音交互满足人们的部分需求.经市场调查,某种新型智能音箱的广告费支出x(万元)与销售额y(单位:万元)之间有如下对应数据:
x | 1 | 4 | 5 | 6 | 9 |
y | 20 | 35 | 50 | 65 | 80 |
(1)求y关于x的线性回归方程(数据精确到0.01);
(2)利用(1)中的回归方程,预测广告费支出10万元时的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为: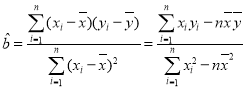 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com