
【题目】中国古代的四书是指:《大学》、《中庸》、《论语》、《孟子》,甲、乙、丙、丁![]() 名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则
名同学从中各选一书进行研读,已知四人选取的书恰好互不相同,且甲没有选《中庸》,乙和丙都没有选《论语》,则![]() 名同学所有可能的选择有______种.
名同学所有可能的选择有______种.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】图①是一栋新农村别墅,它由上部屋顶和下部主体两部分组成.如图②,屋顶由四坡屋面构成,其中前后两坡屋面ABFE和CDEF是全等的等腰梯形,左右两坡屋面EAD和FBC是全等的三角形.点F在平面ABCD和BC上的射影分别为H,M.已知HM 5 m,BC 10 m,梯形ABFE的面积是△FBC面积的2.2倍.设∠FMH ![]()
![]() .
.
(1)求屋顶面积S关于![]() 的函数关系式;
的函数关系式;
(2)已知上部屋顶造价与屋顶面积成正比,比例系数为k(k为正的常数),下部主体造价与其 高度成正比,比例系数为16 k.现欲造一栋上、下总高度为6 m的别墅,试问:当![]() 为何值时,总造价最低?
为何值时,总造价最低?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)当m=1时,求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村共有100户农民,且都从事蔬菜种植,平均每户的年收入为2万元.为了调整产业结构,该镇政府决定动员部分农民从事蔬菜加工.据估计,若能动员![]() 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入比上一年提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入比上一年提高![]() ,而从事蔬菜加工的农民平均每户的年收入为
,而从事蔬菜加工的农民平均每户的年收入为![]() 万元.
万元.
(1)在动员![]() 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前100户农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前100户农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这100户农民中从事蔬菜加工的农民的总年收入始终不高于从事蔬菜种植的农民的总年收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的所有棱长都相等,平面BB1C1C⊥平面ABC,BC1=C1C.
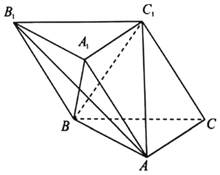
(1)求证:A1B⊥平面AB1C1;
(2)求二面角A1﹣AC1﹣B1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数为( )
(1)![]() 是直线
是直线![]() 和直线
和直线![]() 垂直的充要条件;
垂直的充要条件;
(2)在线性回归方程中,相关系数![]() 越大,变量间的相关性越强;
越大,变量间的相关性越强;
(3)已知随机变量![]() ,若
,若![]() ,则
,则![]()
(4)若命题![]() ,
,![]() ,则
,则![]() ,
,![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新冠肺炎疫情造成医用防护服紧缺,当地政府决定为防护服生产企业A公司扩大生产提供![]() (万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到
(万元)的专项补贴,并以每套80元的价格收购其生产的全部防护服.A公司在收到政府x(万元)补贴后,防护服产量将增加到![]() (万件),其中k为工厂工人的复工率
(万件),其中k为工厂工人的复工率![]() ,A公司生产t万件防护服还需投入成本
,A公司生产t万件防护服还需投入成本![]() (万元).
(万元).
(1)将A公司生产防护服的利润y(万元)表示为补贴x(万元)的函数;
(2)对任意的![]() (万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01)
(万元),当复工率k达到多少时,A公司才能不产生亏损?(精确到0.01)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com