
【题目】如图所示,已知多面体![]() 中,四边形
中,四边形![]() 为矩形,
为矩形, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
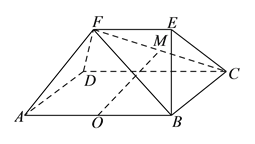
(![]() )求证:
)求证: ![]() .
.
(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )若过
)若过![]() 的平面交
的平面交![]() 于点
于点![]() ,交
,交![]() 于
于![]() ,求证:
,求证: ![]() .
.
【答案】(1)见解析;(2) 见解析(3)见解析
【解析】试题分析:
(1)由平面![]() 平面
平面![]() 可得
可得![]() 平面
平面![]() ,从而
,从而![]() 。又
。又![]() ,可得
,可得![]() 平面
平面![]() ,故得
,故得![]() .(2)取
.(2)取![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() ,可证得四边形
,可证得四边形![]() 是平行四边形,故
是平行四边形,故![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() .(3)由线面平行的性质及平行的传递性可得结论成立。
.(3)由线面平行的性质及平行的传递性可得结论成立。
试题解析:
(![]() )证明:∵ 平面
)证明:∵ 平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
,
∴ ![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴ ![]() ,
,
又![]() ,
, ![]() ,
, ![]() 、
、![]() 平面
平面![]() ,
,
∴ ![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴ ![]() .
.
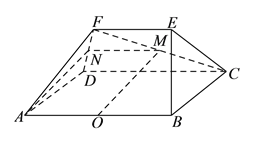
(![]() )证明:取
)证明:取![]() 中点为
中点为![]() ,连接
,连接![]() ,
, ![]() ,
,
∵ ![]() 、
、![]() 分别为
分别为![]() ,
, ![]() 中点,
中点,
∴ ![]()
![]() ,
,
∴ ![]()
∴ 四边形![]() 是平行四边形,
是平行四边形,
∴ ![]() ,
,
∴ ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴ ![]() 平面
平面![]() .
.
(![]() )证明:∵
)证明:∵ ![]() ,
,
∴ 过直线![]() 存在一个平面
存在一个平面![]() ,使得平面
,使得平面![]() 平面
平面![]() ,
,
又过![]() 的平面交
的平面交![]() 于
于![]() 点,交
点,交![]() 于
于![]() 点,
点, ![]() 平面
平面![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.


科目:高中数学 来源: 题型:
【题目】已知三棱锥S﹣ABC的各顶点都在一个半径为r的球面上,且SA=SB=SC=1,AB=BC=AC=![]() ,则球的表面积为( )
,则球的表面积为( )
A. 12π B. 8π C. 4π D. 3π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 为偶函数,对于函数
为偶函数,对于函数![]() 有下列几种描述:
有下列几种描述:
①![]() 是周期函数; ②
是周期函数; ②![]() 是它的一条对称轴;
是它的一条对称轴;
③![]() 是它图象的一个对称中心; ④当
是它图象的一个对称中心; ④当![]() 时,它一定取最大值;
时,它一定取最大值;
其中描述正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2![]() cos
cos![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(1)求圆心的极坐标;
(2)求△PAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有9本不同的课外书,分给甲、乙、丙三名同学,求在下列条件下,各有多少种分法?
(1)甲得4本,乙得3本,丙得2本;
(2)一人得4本,一人得3本,一人得2本;
(3)甲、乙、丙各得3本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由实数组成的等比数列{an}的前项和为Sn , 且满足8a4=a7 , S7=254.
(1)求数列{an}的通项公式;
(2)对n∈N* , bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com