
【题目】设x,y满足约束条件 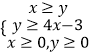 ,若目标函数2z=2x+ny(n>0),z的最大值为2,则y=tan(nx+
,若目标函数2z=2x+ny(n>0),z的最大值为2,则y=tan(nx+ ![]() )的图象向右平移
)的图象向右平移 ![]() 后的表达式为( )
后的表达式为( )
A.y=tan(2x+ ![]() )
)
B.y=tan(x﹣ ![]() )
)
C.y=tan(2x﹣ ![]() )
)
D.y=tan2x
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】已知命题 ![]() “存在
“存在 ![]() ”,命题
”,命题 ![]() :“曲线
:“曲线 ![]() 表示焦点在
表示焦点在 ![]() 轴上的椭圆”,命题
轴上的椭圆”,命题 ![]() “曲线
“曲线 ![]() 表示双曲线”
表示双曲线”
(1)若“ ![]() 且
且 ![]() ”是真命题,求实数
”是真命题,求实数 ![]() 的取值范围;
的取值范围;
(2)若 ![]() 是
是 ![]() 的必要不充分条件,求实数
的必要不充分条件,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足:a1=![]() ,a2=2,3(an+1-2an+an-1)=2.
,a2=2,3(an+1-2an+an-1)=2.
(1)证明:数列{an+1-an}是等差数列;
(2)求使![]() +…+
+…+![]() 成立的最小的正整数n.
成立的最小的正整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统综》是明朝程大位所著数学名著,其中有这样一段表述:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一”,其意大致为:有一七层宝塔,每层悬挂的红灯数为上一层的两倍,共有381盏灯,则塔从上至下的第三层有( )盏灯.
A.14
B.12
C.10
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线 ![]() 的焦点F,斜率为
的焦点F,斜率为 ![]() 的直线交抛物线于
的直线交抛物线于 ![]() 两点,且
两点,且 ![]() .
.
(1)求该抛物线E的方程;
(2)过点F任意作互相垂直的两条直线 ![]() ,分别交曲线E于点C,D和M,N.设线段
,分别交曲线E于点C,D和M,N.设线段 ![]() 的中点分别为P,Q,求证:直线PQ恒过一个定点.
的中点分别为P,Q,求证:直线PQ恒过一个定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com