Question

15．若∠APB=∠BPC=∠CPA=60°，则直线PA与平面PBC所成角的余弦值为$\frac{\sqrt{3}}{3}$．

Answer 1

分析 在PA上任选一点Q，过Q作QO⊥平面PBC于O点，连结PO，说明∠QPO即为PA与平面PBC所成的角，通过求解三角形的数据求解cos∠APO．

解答 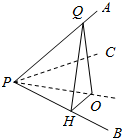解：如图所示，在PA上任选一点Q
过Q作QO⊥平面PBC于O点，连结PO由于∠APB=∠APC=60°
∴PO为∠BPC的平分线，∠QPO即为PA与平面PBC所成的角
∠BPO=30°
作OH⊥PB于H，连QH
根据三垂线定理，QH⊥PH
RT△QPH中，∠QPH=60°，PQ=2PH
RT△OPH中，PO=$\frac{2\sqrt{3}}{3}PH$
RT△QPO中
cos∠APO=$\frac{PO}{QP}$=$\frac{\frac{2\sqrt{3}}{3}PH}{2PH}$=$\frac{\sqrt{3}}{3}$．
故答案为：$\frac{\sqrt{3}}{3}$．

点评 本题考查直线与平面所成角的求法，考查空间想象能力以及计算能力．