
【题目】已知椭圆![]() 的中心在坐标原点,两焦点分别为双曲线
的中心在坐标原点,两焦点分别为双曲线![]() 的顶点,直线
的顶点,直线![]() 与椭圆
与椭圆![]() 交于A,B两点,且点A的坐标为
交于A,B两点,且点A的坐标为![]() ,点Р是椭圆
,点Р是椭圆![]() 上异于A,B的任意一点,点Q满足
上异于A,B的任意一点,点Q满足![]() ,
,![]() ,且A,B,Q三点不共线.
,且A,B,Q三点不共线.
(1)求椭圆![]() 的方程;
的方程;
(2)求点Q的轨迹方程.
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的中心为原点,焦点
的中心为原点,焦点![]() ,
,![]() 在
在![]() 轴上,离心率为
轴上,离心率为![]() .过
.过![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)圆![]() 与
与![]() 轴正半轴相交于两点
轴正半轴相交于两点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),过点
的左侧),过点![]() 任作一条直线与椭圆
任作一条直线与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,连接
两点,连接![]() ,
,![]() ,求证
,求证![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】不等式组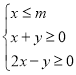 表示的平面区域为D,
表示的平面区域为D,![]() 的最大值等于8.
的最大值等于8.
(1)求![]() 的值;
的值;
(2)求![]() 的取值范围;
的取值范围;
(3)若直线![]() 过点P(-3,3),求区域D在直线
过点P(-3,3),求区域D在直线![]() 上的投影的长度的取值范围.
上的投影的长度的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
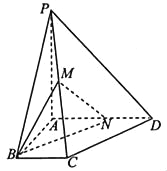
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M为PC的中点点N在线段AD上.
(1)点N为线段AD的中点时,求证:直线PA∥面BMN;
(2)若直线MN与平面PBC所成角的正弦值为![]() ,求二面角C﹣BM﹣N所成角θ的余弦值.
,求二面角C﹣BM﹣N所成角θ的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,双曲线![]() :
:![]() 经过点
经过点![]() ,其中一条近线的方程为
,其中一条近线的方程为![]() ,椭圆
,椭圆![]() :
:![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 椭圆
椭圆![]() 的左焦点,左顶点和上顶点分别为F,A,B,且点F到直线AB的距离为
的左焦点,左顶点和上顶点分别为F,A,B,且点F到直线AB的距离为![]() .
.
![]() 求双曲线
求双曲线![]() 的方程;
的方程;
![]() 求椭圆
求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某基地蔬菜大棚采用无土栽培方式种植各类蔬菜.根据过去50周的资料显示,该基地周光照量![]() (小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量![]() (千克)与使用某种液体肥料的质量
(千克)与使用某种液体肥料的质量![]() (千克)之间的关系如图所示.
(千克)之间的关系如图所示.

(1)依据上图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01).(若
并加以说明(精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 |
|
|
|
光照控制仪运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.以频率作为概率,商家欲使周总利润的均值达到最大,应安装光照控制仪多少台?
附:相关系数公式 ,
,
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教材中指出:当![]() 很小,
很小,![]() 不太大时,可以用
不太大时,可以用![]() 表示
表示![]() 的近似值,即
的近似值,即![]() (1),我们把近似值与实际值之差除以实际值的商的绝对值称为“相对近似误差”,一般用字母
(1),我们把近似值与实际值之差除以实际值的商的绝对值称为“相对近似误差”,一般用字母![]() 表示,即相对近似误差
表示,即相对近似误差![]()
(1)利用(1)求出![]() 的近似值,并指出其相对近似误差(相对近似误差保留两位有效数字)
的近似值,并指出其相对近似误差(相对近似误差保留两位有效数字)
(2)若利用(1)式计算![]() 的近似值产生的相对近似误差不超过
的近似值产生的相对近似误差不超过![]() ,求正实数
,求正实数![]() 的取值范围;
的取值范围;
(3)若利用(1)式计算![]() 的近似值产生的相对近似误差不超过
的近似值产生的相对近似误差不超过![]() ,求正整数
,求正整数![]() 的最大值。(参考对数数值:
的最大值。(参考对数数值:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com