
设不等式组 所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n)(n∈N*).
所表示的平面区域为Dn,记Dn内的格点(格点即横坐标和纵坐标均为整数的点)个数为f(n)(n∈N*).
(1)求f(1),f(2)的值及f(n)的表达式;
(2)记![]() ,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围;
,若对于一切正整数n,总有Tn≤m成立,求实数m的取值范围;
(3)设Sn为数列{bn}的前n项和,其中bn=2f(n),问是否存在正整数n,t,使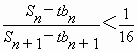 成立?若存在,求出正整数n,t;若不存在,说明理由.
成立?若存在,求出正整数n,t;若不存在,说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:广东省培正中学2011-2012学年高二第一学期期中考考试数学理科试题 题型:044
已知(x,y)(x,y∈R)为平面上点M的坐标.
(1)设集合P={―4,―3,―2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中随机取一个数作为y,求点M在y轴上的概率;
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组: 所表示的平面区域内的概率.
所表示的平面区域内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com