练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    命题“若△不是等腰三角形，则它的任何两个内角不相等”的逆否命题              是                                                               ；
    若△的两个内角相等，则它是等腰三角形
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    有下列几个命题：①若
    a
    与
    b
    -
    c
    都是非零向量，则“
    a
    •
    b
    =
    a
    •
    c
    ”是“
    a
    ⊥(
    b
    -
    c
    )    ”的充要条件；②已知等腰△ABC的腰为底的2倍，则顶角A的正切值是
    		15
    7
    ；③在平面直角坐标系xoy中，四边形ABCD的边AB∥DC，AD∥BC，已知点A（-2，0），B（6，8），C（8，6），则D点的坐标为（0，-1）；④设
    a
    ，
    b
    ，
    c
    为同一平面内具有相同起点的任意三个非零向量，且满足
    a
    与
    b
    不共线，
    a
    ⊥
    c
    ，|
    a
    |=|
    c
    |，则|
    b
    •
    c
    |的值一定等于以
    a
    ，
    b
    为邻边的平行四边形的面积．其中正确命题的序号是
     
    ．（写出全部正确结论的序号）

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年河南省卫辉市高三2月月考数学理卷 题型：选择题

    下列命题中不正确命题的个数是（　　）

    ①经过空间一点一定可作一平面与两异面直线都平行；

    ②已知平面、，直线a、b，若，，则；

    ③有两个侧面垂直于底面的四棱柱为直四棱柱；

    ④四个侧面两两全等的四棱柱为直四棱柱；

    ⑤底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；

    ⑥底面是等边三角形，∠APB＝∠BPC＝∠CPA，则三棱锥P－ABC是正三棱锥.

    A．0                               B．1           C．2                             D．3

     

    查看答案和解析>>

    科目：高中数学 来源：2010年江西省高二第一次段考理科数学试卷 题型：填空题

    以下命题正确的是                 

    ①在空间中，若四点不共面，则这四点中任何三点都不共线的逆命题是真命题。

    ②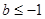是方程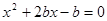有实数解的充要条件。

    ③若函数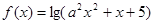的值域为全体实数，则有。

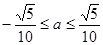    ④在△ABC中，若tanAsin2B=tanBsin2A，则△ABC为等腰直角三角形

    ⑤在△ABC中，a、b、c分别是∠A、∠B、∠C所对边，C=90°，则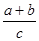的取值范围为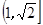

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    有下列几个命题：①若
    a
    与
    b
    -
    c
    都是非零向量，则“
    a
    •
    b
    =
    a
    •
    c
    ”是“
    a
    ⊥(
    b
    -
    c
    )    ”的充要条件；②已知等腰△ABC的腰为底的2倍，则顶角A的正切值是
    		15
    7
    ；③在平面直角坐标系xoy中，四边形ABCD的边AB∥DC，AD∥BC，已知点A（-2，0），B（6，8），C（8，6），则D点的坐标为（0，-1）；④设
    a
    ，
    b
    ，
    c
    为同一平面内具有相同起点的任意三个非零向量，且满足
    a
    与
    b
    不共线，
    a
    ⊥
    c
    ，|
    a
    |=|
    c
    |，则|
    b
    •
    c
    |的值一定等于以
    a
    ，
    b
    为邻边的平行四边形的面积．其中正确命题的序号是______．（写出全部正确结论的序号）

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年北京大学附中高三（上）数学练习试卷4（文科）（解析版） 题型：填空题

    有下列几个命题：①若与都是非零向量，则“”是“”的充要条件；②已知等腰△ABC的腰为底的2倍，则顶角A的正切值是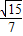；③在平面直角坐标系xoy中，四边形ABCD的边AB∥DC，AD∥BC，已知点A（-2，0），B（6，8），C（8，6），则D点的坐标为（0，-1）；④设，，为同一平面内具有相同起点的任意三个非零向量，且满足与不共线，⊥，||=||，则|•|的值一定等于以，为邻边的平行四边形的面积．其中正确命题的序号是    ．（写出全部正确结论的序号）

    查看答案和解析>>

    同步练习册答案