
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为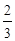 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为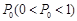 ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为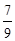 ,求
,求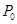 ;
;
(2)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
(1)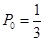 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)记“这2人的累计得分X≤3”的事件为A,依题意,两人累计得分的可能值为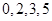 ,故事件“
,故事件“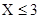 ”的对立事件为“
”的对立事件为“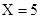 ”,所以所求事件的概率
”,所以所求事件的概率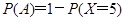 ;(2)因为每次抽奖中奖与否互不影响,且对方案甲或方案乙而言,中奖的概率不变,故对于张三、李四两人抽奖可看成两次独立重复试验,其中奖次数服从二项分布,设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,则X1~
;(2)因为每次抽奖中奖与否互不影响,且对方案甲或方案乙而言,中奖的概率不变,故对于张三、李四两人抽奖可看成两次独立重复试验,其中奖次数服从二项分布,设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,则X1~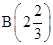 ,X2~B
,X2~B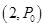 ,则累计得分的期望为E(2X1),E(3X2),从而比较大小即可.
,则累计得分的期望为E(2X1),E(3X2),从而比较大小即可.
(1)由已知得,张三中奖的概率为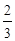 ,李四中奖的概率为
,李四中奖的概率为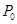 ,且两人中奖与否互不影响.
,且两人中奖与否互不影响.
记“这2人的累计得分X≤3”的事件为A,则事件A的对立事件为“X=5”,
因为
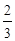 ×
×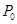 ,所以
,所以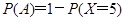 =1-
=1-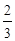 ×
×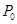 =
= ,所以
,所以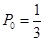 . 6分
. 6分
(2)设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,
则这两人选择方案甲抽奖累计得分的数学期望为E(2X1),
选择方案乙抽奖累计得分的数学期望为E(3X2).
由已知可得,X1~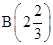 ,X2~B
,X2~B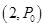 ,
,
所以E(X1)=2×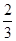 =
=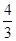 ,E(X2)=2×
,E(X2)=2×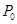 ,
,
从而E(2X1)=2E(X1)=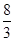 ,E(3X2)=3E(X2)=6
,E(3X2)=3E(X2)=6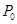 .
.
若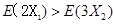 ,即
,即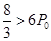 ,所以
,所以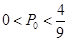 ;
;
若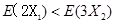 ,即
,即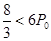 ,所以
,所以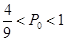 ;
;
若 ,即
,即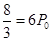 ,所以
,所以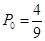 .
.
综上所述:当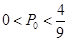 时,他们都选择方案甲进行抽奖时,累计得分的数学期望较大;当
时,他们都选择方案甲进行抽奖时,累计得分的数学期望较大;当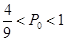 时,他们都选择方案乙进行抽奖时,累计得分的数学期望较大;当
时,他们都选择方案乙进行抽奖时,累计得分的数学期望较大;当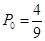 时,他们都选择方案甲或乙进行抽奖时,累计得分的数学期望相等. 12分
时,他们都选择方案甲或乙进行抽奖时,累计得分的数学期望相等. 12分
考点:1、对立事件;2、二项分布的期望.


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:解答题
小王参加一次比赛,比赛共设三关,第一、二关各有两个必答题,如果每关两个问题都答对,可进入下一关,第三关有三个问题,只要答对其中两个问题,则闯关成功.每过一关可一次性获得价值分别为1000元,3000元,6000元的奖品(不重复得奖),小王对三关中每个问题回答正确的概率依次为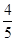 ,
,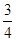 ,
,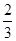 ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.
(1)求小王过第一关但未过第二关的概率;
(2)用X表示小王所获得奖品的价值,写出X的概率分布列,并求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为: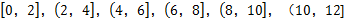 .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.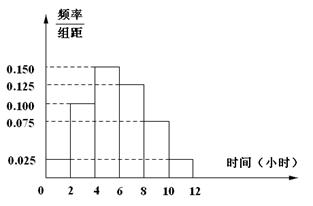
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有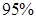 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
附: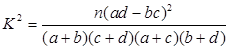
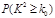 | 0.10 | 0.05 | 0.010 | 0.005 |
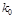 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为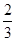 和
和 ,现安排甲组研发新产品
,现安排甲组研发新产品 ,乙组研发新产品
,乙组研发新产品 .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品 研发成功,预计企业可获得
研发成功,预计企业可获得 万元,若新产品
万元,若新产品 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
第十二届全国人民代表大会第二次会议和政协第十二届全国委员会第二次会议,2014年3月在北京召开.为了做好两会期间的接待服务工作,中国人民大学学生实践活动中心从7名学生会干部(其中男生4人,女生3人)中选3人参加两会的志愿者服务活动.
(1)所选3人中女生人数为 ,求
,求 的分布列及数学期望:
的分布列及数学期望:
(2)在男生甲被选中的情况下,求女生乙也被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表是某市从3月份中随机抽取的 天空气质量指数(
天空气质量指数( )和“
)和“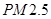 ”(直径小于等于
”(直径小于等于 微米的颗粒物)
微米的颗粒物) 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数( )小于
)小于 表示空气质量优良.
表示空气质量优良.
| 日期编号 |  |  |  |  |  |  |  |  |  |  |
空气质量指数( ) ) |  |  |  |  |  |  |  |  |  |  |
“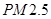 ” ” 小时平均浓度( 小时平均浓度(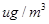 ) ) |  |  |  |  |  |  |  |  |  |  |
 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘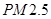 ’的
’的 小时平均浓度不超过
小时平均浓度不超过 ”,求事件
”,求事件 发生的概率.
发生的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•天津)一个盒子里装有7张卡片,其中有红色卡片4张,编号分别为1,2,3,4; 白色卡片3张,编号分别为2,3,4.从盒子中任取4张卡片 (假设取到任何一张卡片的可能性相同).
(1)求取出的4张卡片中,含有编号为3的卡片的概率.
(2)再取出的4张卡片中,红色卡片编号的最大值设为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两射手在同一条件下进行射击,分布列如下:射手甲击中环数8,9,10的概率分别为0.2,0.6,0.2;射手乙击中环数8,9,10的概率分别为0.4,0.2,0.4.用击中环数的期望与方差比较两名射手的射击水平.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2011•山东)甲、乙两校各有3名教师报名支教,期中甲校2男1女,乙校1男2女.
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com