
【题目】如图,在三棱柱 ![]() 中,
中, ![]() 底面
底面 ![]() ,且
,且 ![]() 为等边三角形,
为等边三角形, ![]() ,
, ![]() 为
为 ![]() 的中点.
的中点.
(1)求证:直线 ![]() 平面
平面 ![]() ;
;
(2)求证:平面 ![]() 平面
平面 ![]() ;
;
(3)求三棱锥 ![]() 的体积.
的体积.
【答案】
(1)证明:如图所示
连接 ![]() 交
交 ![]() 于
于 ![]() ,连接
,连接 ![]()
因为四边形 ![]() 是平行四边形,
是平行四边形,
所以 ![]() 为
为 ![]() 的中点,
的中点,
又因为 ![]() 为
为 ![]() 的中点,
的中点,
所以 ![]() 为
为 ![]() 的中位线,
的中位线,
所以 ![]()
又 ![]() 平面
平面 ![]() 平面
平面 ![]() ,
,
所以 ![]() 平面
平面 ![]() .
.
(2)证明:因为 ![]() 是等边三角形,
是等边三角形, ![]() 为
为 ![]() 的中点,
的中点,
所以 ![]()
又因为 ![]() 底面
底面 ![]()
所以 ![]()
根所线面垂直的判定定理得 ![]() 平面
平面 ![]()
又因为 ![]() 平面
平面 ![]()
所以平面 ![]() 平面
平面 ![]() ;
;
(3)解:由(2)知, ![]() 中,
中, ![]()
![]()
![]()
![]()

【解析】(1)由题意构造平面BC1D内的直线,再证明直线AB1与这条直线平行。(2)根据线面垂直的判定定理即可得证。(3)根据题意利用等体积法即可求出体积。
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】锐角△ABC中,角A,B,C的对边分别为a,b,c,向量 ![]() ,
, ![]() ,且
,且 ![]() .
.
(1)求角B的大小;
(2)若sinAsinC=sin2B,求a﹣c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax+bx+cx , 其中c>a>0,c>b>0,若a,b,c是△ABC的三条边长,则下列结论正确的是( ) ①对任意x∈(﹣∞,1),都有f(x)<0;
②存在x∈R,使ax , bx , cx不能构成一个三角形的三条边长;
③若△ABC为钝角三角形,存在x∈(1,2),使f(x)=0.
A.①②
B.②③
C.①③
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列选项中,说法正确的是( )
A.若a>b>0,则 ![]()
B.向量 ![]() (m∈R)共线的充要条件是m=0
(m∈R)共线的充要条件是m=0
C.命题“?n∈N* , 3n>(n+2)?2n﹣1”的否定是“?n∈N* , 3n≥(n+2)?2n﹣1”
D.已知函数f(x)在区间[a,b]上的图象是连续不断的,则命题“若f(a)?f(b)<0,则f(x)在区间(a,b)内至少有一个零点”的逆命题为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D. 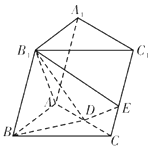
(1)求证:平面ABB1A1⊥平面ABC;
(2)在线段CC1(不含端点)上,是否存在点E,使得二面角E﹣B1D﹣B的余弦值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:k2﹣8k﹣20≤0,命题q:方程 ![]() =1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
=1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
(Ⅱ)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com