练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在△ABC中，∠C=90°，|AC|=b，|BC|=a （a＞b），A、B分别在x轴，y轴的正半轴上滑动，且A、B、C按顺时针方向排列，求顶点C的轨迹．

    解：在△ABC中，∠C=90°，|AC|=b，|BC|=a （a＞b），A、B分别在x轴，y轴的正半轴上滑动，设C（x，y）AB的中点为：Q（），
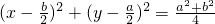
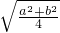
    所以，|QC|=|AB|，即：，因为A、B、C按顺时针方向排列，所以顶点C的轨迹是以Q（）为圆心，以为半径的圆，在直线AB的上方的半圆，不包含A、B两个点．
    分析：设出顶点C的坐标，由题意求出AB的中点Q的坐标，|QC|=|AB|可得顶点C的轨迹．
    点评：本题是中档题，考查轨迹方程的求法，注意条件的转化，条件的挖掘和应用，注意除去不满足题意的轨迹．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在△ABC中，∠C=60°，a，b，c分别为∠A、∠B、∠C的对边，则
    a
    b+c
    +
    b
    c+a
    =
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，∠C=90°，
    AB
    =(1，k)    ，
    AC
    =(2，1)    ，则k的值是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    命题p：在△ABC中，∠C＞∠B是sinC＞sinB的充分不必要条件；命题q：a＞b是ac2＞bc2的充分不必要条件．则（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，∠C=90°，BC=
    1
    2
    AB，则
    AB
    与
    BC
    与的夹角是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•嘉兴二模）如图，在△ABC中，∠C=90°，AC=BC=3a，点P在AB上，PE∥BC交AC于E，PF∥AC交BC于F．沿PE将△APE翻折成△A′PE，使平面A′PE⊥平面ABC；沿PF将△BPF翻折成△B′PF，使平面B′PF⊥平面ABC．
    （Ⅰ）求证：B′C∥平面A′PE．
    （Ⅱ）若AP=2PB，求二面角A′-PC-E的平面角的正切值．

    查看答案和解析>>

    同步练习册答案