
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
分析 (1)根据所给的数据,做出变量x,y的平均数,根据最小二乘法做出线性回归方程的系数b,在根据样本中心点一定在线性回归直线上,求出a的值.
(2)根据第一问做出的a,b的值,写出线性回归方程,当自变量为10时,代入线性回归方程,求出维修费用,这是一个预报值.
解答 解:(1)根据题表中数据作散点图,如图所示: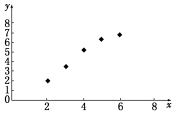
从散点图可以看出,样本点都集中分布在一条直线附近,因此y与x之间具有线性相关关系.利用题中数据得:
$\overline{x}$=$\frac{1}{5}$(2+3+4+5+6)=4,
$\overline{y}$=$\frac{1}{5}$(2.2+3.8+5.5+6.5+7.0)=5,
$\sum_{i=1}^{n}$xiyi=2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3,
$\sum_{i=1}^{5}$${{x}_{i}}^{2}$=22+32+42+52+62=90,
所以$\widehat{b}$=$\frac{112.3-5×4×5}{90-5{×4}^{2}}$=1.23,
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=0.08,
∴线性回归方程为$\widehat{y}$=1.23x+0.08.
(2)当x=10时,$\widehat{y}$=1.23×10+0.08=12.38(万元),
即当使用10年时,估计维修费用是12.38万元.
点评 本题考查线性回归方程,考查最小二乘法,考查预报值的求法,是一个新课标中出现的新知识点,已经在广东的高考卷中出现过类似的题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图,建立平面直角坐标系xoy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-$\frac{1}{20}$(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
如图,建立平面直角坐标系xoy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-$\frac{1}{20}$(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?p:?x∈R,sinx≤1 | B. | ?p:?x∈R,sinx≤1 | C. | ?p:?x∈R,sinx≤1 | D. | ?p:?x∈R,sinx>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n-1 | B. | ${(\frac{1}{2})^{n-1}}$ | C. | ${(\frac{2}{3})^{n-1}}$ | D. | ${(\frac{3}{2})^{n-1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
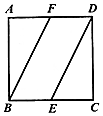 如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )
如图,在正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在直线进行翻折,将△CDE沿DE所在直线进行翻折,在翻折的过程中( )| A. | 点A与点C在某一位置可能重合 | B. | 点A与点C的最大距离为$\sqrt{3}$AB | ||
| C. | 直线AB与直线CD可能垂直 | D. | 直线AF与直线CE可能垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com