
【题目】如图,已知多面体![]() ,其底面
,其底面![]() 为矩形,四边形
为矩形,四边形![]() 为平行四边形,平面
为平行四边形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
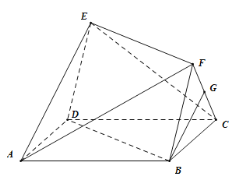
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)证明见详解;(2)![]()
【解析】
(1)取![]() 中点
中点![]() ,
,![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,推到出四边形
,推到出四边形![]() 是平行四边形,从而
是平行四边形,从而![]() ,推到出四边形
,推到出四边形![]() 是平行四边形,从而
是平行四边形,从而![]() ,
,![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
(2)直线![]() 与平面
与平面![]() 所成角即等于直线
所成角即等于直线![]() 与平面
与平面![]() 所成角,作
所成角,作![]() ,
,![]() ,连接
,连接![]() ,则
,则![]() 平面
平面![]() ,从而
,从而![]() 点到平面
点到平面![]() 的距离等于
的距离等于![]() 点平面
点平面![]() 的距离
的距离![]() ,由等面积法求出
,由等面积法求出![]() ,由此能求出直线
,由此能求出直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
(1)取![]() 中点
中点![]() ,
,![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,
,
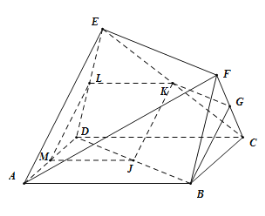
![]()
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]()
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]()
(2)由(1)知,
直线![]() 与平面
与平面![]() 所成角,
所成角,
即等于直线![]() 与平面
与平面![]() 所成角,
所成角,
作![]() ,
,![]() ,连接
,连接![]() ,
,
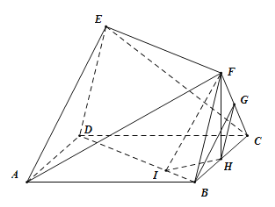
![]()
![]() 都是所在棱的中点,
都是所在棱的中点,![]() 平面
平面![]() ,
,
![]()
![]() 点到平面
点到平面![]() 的距离等于
的距离等于![]() 点平面
点平面![]() 的距离
的距离![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
由等面积法可知: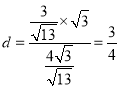 ,
,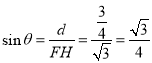 ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,设点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且它们的斜率之积为
,且它们的斜率之积为![]() .
.
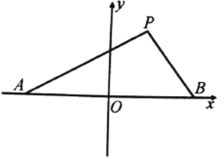
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为
的轨迹为![]() ,点
,点![]() 是轨迹为
是轨迹为![]() 上不同于
上不同于![]() 的两点,且满足
的两点,且满足![]() ,求证:
,求证:![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】法国数学家庞加是个喜欢吃面包的人,他每天都会购买一个面包,面包师声称自己出售的每个面包的平均质量是1000![]() ,上下浮动不超过50
,上下浮动不超过50![]() .这句话用数学语言来表达就是:每个面包的质量服从期望为1000
.这句话用数学语言来表达就是:每个面包的质量服从期望为1000![]() ,标准差为50
,标准差为50![]() 的正态分布.
的正态分布.
(1)假设面包师的说法是真实的,从面包师出售的面包中任取两个,记取出的两个面包中质量大于1000![]() 的个数为
的个数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)作为一个善于思考的数学家,庞加莱每天都会将买来的面包称重并记录,25天后,得到数据如下表,经计算25个面包总质量为24468![]() .庞加莱购买的25个面包质量的统计数据(单位:
.庞加莱购买的25个面包质量的统计数据(单位:![]() )
)
981 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 | 978 |
989 | 1001 | 1006 | 957 | 952 | 969 | 981 | 984 | 952 | 959 |
987 | 1006 | 1000 | 977 | 966 |
尽管上述数据都落在![]() 上,但庞加菜还是认为面包师撒谎,根据所附信息,从概率角度说明理由
上,但庞加菜还是认为面包师撒谎,根据所附信息,从概率角度说明理由
附:
①若![]() ,从X的取值中随机抽取25个数据,记这25个数据的平均值为Y,则由统计学知识可知:随机变量
,从X的取值中随机抽取25个数据,记这25个数据的平均值为Y,则由统计学知识可知:随机变量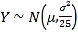
②若![]() ,则
,则![]() ,
,![]() ,
,![]() ;
;
③通常把发生概率在0.05以下的事件称为小概率事件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商家通常依据“乐观系数准则”确定商品销售价格,及根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b﹣a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c﹣a)是(b﹣c)和(b﹣a)的等比中项,据此可得,最佳乐观系数x的值等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别为
分别为![]() 内角
内角![]() 的对边,若
的对边,若![]() 是锐角三角形,需要同时满足下列四个条件中的三个:
是锐角三角形,需要同时满足下列四个条件中的三个:
①![]() ②
②![]() ③
③![]() ④
④![]()
(1)条件①④能否同时满足,请说明理由;
(2)以上四个条件,请在满足三角形有解的所有组合中任选一组,并求出对应的![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年女排世界杯(第13届女排世界杯)是由国际排联![]() 举办的赛事,比赛于2019年9月14日至9月29日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球
举办的赛事,比赛于2019年9月14日至9月29日在日本举行,共有12支参赛队伍.本次比赛启用了新的排球用球![]() _
_![]() ,已知这种球的质量指标ξ(单位:
,已知这种球的质量指标ξ(单位:![]() )服从正态分布
)服从正态分布![]() .比赛赛制采取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以
.比赛赛制采取单循环方式,即每支球队进行11场比赛,最后靠积分选出最后冠军.积分规则如下(比赛采取5局3胜制):比赛中以![]() 或
或![]() 取胜的球队积3分,负队积0分;而在比赛中以
取胜的球队积3分,负队积0分;而在比赛中以![]() 取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为
取胜的球队积2分,负队积1分.9轮过后,积分榜上的前2名分别为中国队和美国队,中国队积26分,美国队积22分.第10轮中国队对抗塞尔维亚队,设每局比赛中国队取胜的概率为![]() .
.
(1)如果比赛准备了1000个排球,估计质量指标在![]() 内的排球个数(计算结果取整数)
内的排球个数(计算结果取整数)
(2)第10轮比赛中,记中国队![]() 取胜的概率为
取胜的概率为![]() ,求出
,求出![]() 的最大值点
的最大值点![]() ,并以
,并以![]() 作为p的值,解决下列问题.
作为p的值,解决下列问题.
(i)在第10轮比赛中,中国队所得积分为X,求X的分布列;
(ii)已知第10轮美国队积3分,判断中国队能否提前一轮夺得冠军(第10轮过后,无论最后一轮即第11轮结果如何,中国队积分最多)?若能,求出相应的概率;若不能,请说明理由.
参考数据:![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com