
【题目】如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( ) 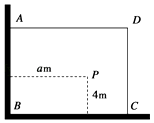
A.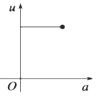
B.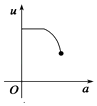
C.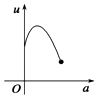
D.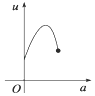
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin2x+cos2(
sin2x+cos2( ![]() ﹣x)﹣
﹣x)﹣ ![]() (x∈R).
(x∈R).
(1)求函数f(x)在区间[0, ![]() ]上的最大值;
]上的最大值;
(2)在△ABC中,若A<B,且f(A)=f(B)= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市A(看做一点)的东偏南θ角方向 ![]() ,300km的海面P处,并以20km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大.
,300km的海面P处,并以20km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大. 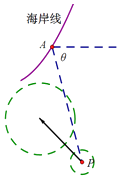
(1)问10小时后,该台风是否开始侵袭城市A,并说明理由;
(2)城市A受到该台风侵袭的持续时间为多久?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2|x+2|﹣|x+1|,无穷数列{an}的首项a1=a.
(1)如果an=f(n)(n∈N*),写出数列{an}的通项公式;
(2)如果an=f(an﹣1)(n∈N*且n≥2),要使得数列{an}是等差数列,求首项a的取值范围;
(3)如果an=f(an﹣1)(n∈N*且n≥2),求出数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sinxcos2x,则下列结论中错误的为( )
A.点(π,0)是函数y=f(x)图象的一个对称中心
B.直线x= ![]() 是函数y=f(x)图象的一条对称轴
是函数y=f(x)图象的一条对称轴
C.π是函数y=f(x)的周期
D.函数y=f(x)的最大值为1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com