
【题目】设不等式组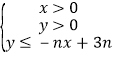 所表示的平面区域为
所表示的平面区域为![]() ,记
,记![]() 内的整点个数为
内的整点个数为![]() ,(整点即横、纵坐标均为整数的点)
,(整点即横、纵坐标均为整数的点)
(1)计算![]() 的值;
的值;
(2)求数列![]() 的通项公式
的通项公式![]() ;
;
(3)记数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,若对于一切的正整数
,若对于一切的正整数![]() ,总有
,总有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某海域有![]() 两个岛屿,
两个岛屿,![]() 岛在
岛在![]() 岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处,经多年观察研究发现,某种鱼群洄游的路线是曲线![]() ,曾有渔船在距
,曾有渔船在距![]() 岛、
岛、![]() 岛距离和为8海里处发出过鱼群。以
岛距离和为8海里处发出过鱼群。以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 的垂直平分线为
的垂直平分线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求曲线![]() 的标准方程;
的标准方程;
(2)某日,研究人员在![]() 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),![]() 两岛收到鱼群在
两岛收到鱼群在![]() 处反射信号的时间比为
处反射信号的时间比为![]() ,问你能否确定
,问你能否确定![]() 处的位置(即点
处的位置(即点![]() 的坐标)?
的坐标)?
查看答案和解析>>
科目:高中数学 来源: 题型:
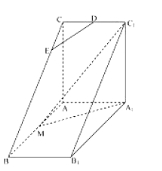
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() ,圆
,圆![]() 的圆心在圆
的圆心在圆![]() 的内部,且直线
的内部,且直线![]() 被圆
被圆![]() 所截得的弦长为
所截得的弦长为![]() .点
.点![]() 为圆
为圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
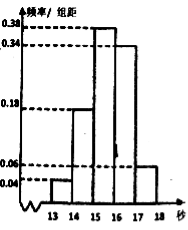
(1)请根据频率分布直方图估计该组数据的众数和中位数(精确到0.1);
(2)从成绩介于![]() 和
和![]() 两组的人中任取2人,求两人分布来自不同组的概率.
两组的人中任取2人,求两人分布来自不同组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com