
【题目】已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,实轴长为6,渐近线方程为
,实轴长为6,渐近线方程为![]() ,动点
,动点![]() 在双曲线左支上,点
在双曲线左支上,点![]() 为圆
为圆![]() 上一点,则
上一点,则![]() 的最小值为
的最小值为
A. 8 B. 9 C. 10 D. 11
【答案】B
【解析】
求得双曲线的a,b,可得双曲线方程,求得焦点坐标,运用双曲线的定义和三点共线取得最小值,连接EF1,交双曲线于M,交圆于N,计算可得所求最小值.
由题意可得2a=6,即a=3,
渐近线方程为y=±![]() x,即有
x,即有![]() ,
,
即b=1,可得双曲线方程为![]() y2=1,
y2=1,
焦点为F1(![]() ,0),F2,(
,0),F2,(![]() ,0),
,0),
由双曲线的定义可得|MF2|=2a+|MF1|=6+|MF1|,
由圆E:x2+(y![]() )2=1可得E(0,
)2=1可得E(0,![]() ),半径r=1,
),半径r=1,
|MN|+|MF2|=6+|MN|+|MF1|,
连接EF1,交双曲线于M,交圆于N,
可得|MN|+|MF1|取得最小值,且为|EF1|![]() 4,
4,
则则|MN|+|MF2|的最小值为6+4﹣1=9.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】太极图被称为“中华第一图”,闪烁着中华文明进程的光辉,它是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐美.定义:能够将圆O的周长和面积同时等分成两个部分的函数称为圆O的一个“太极函数”,设圆O:![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )

A.函数![]() 是圆O的一个太极函数
是圆O的一个太极函数
B.圆O的所有非常数函数的太极函数都不能为偶函数
C.函数![]() 是圆O的一个太极函数
是圆O的一个太极函数
D.函数![]() 的图象关于原点对称是
的图象关于原点对称是![]() 为圆O的太极函数的充要条件
为圆O的太极函数的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 、
、![]() ,线段
,线段![]() 的长为4.点
的长为4.点![]() 在椭圆
在椭圆![]() 上且位于第一象限,过点
上且位于第一象限,过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
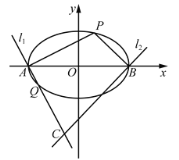
(1)若点![]() 的横坐标为-1,求点
的横坐标为-1,求点![]() 的坐标;
的坐标;
(2)直线![]() 与椭圆
与椭圆![]() 的另一交点为
的另一交点为![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设点![]() ,定义
,定义![]() ,其中
,其中![]() 为坐标原点,对于下列结论:
为坐标原点,对于下列结论:
![]() 符合
符合![]() 的点
的点![]() 的轨迹围成的图形面积为8;
的轨迹围成的图形面积为8;
![]() 设点
设点![]() 是直线:
是直线:![]() 上任意一点,则
上任意一点,则![]() ;
;
![]() 设点
设点![]() 是直线:
是直线:![]() 上任意一点,则使得“
上任意一点,则使得“![]() 最小的点有无数个”的充要条件是
最小的点有无数个”的充要条件是![]() ;
;
![]() 设点
设点![]() 是椭圆
是椭圆![]() 上任意一点,则
上任意一点,则![]() .
.
其中正确的结论序号为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设点![]() ,定义
,定义![]() ,其中
,其中![]() 为坐标原点,对于下列结论:
为坐标原点,对于下列结论:
![]() 符合
符合![]() 的点
的点![]() 的轨迹围成的图形面积为8;
的轨迹围成的图形面积为8;
![]() 设点
设点![]() 是直线:
是直线:![]() 上任意一点,则
上任意一点,则![]() ;
;
![]() 设点
设点![]() 是直线:
是直线:![]() 上任意一点,则使得“
上任意一点,则使得“![]() 最小的点
最小的点![]() 有无数个”的必要条件是
有无数个”的必要条件是![]() ;
;
![]() 设点
设点![]() 是圆
是圆![]() 上任意一点,则
上任意一点,则![]() .
.
其中正确的结论序号为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第三季)亮点颇多,在“人生自有诗意”的主题下,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《沁园春·长沙》、《蜀道难》、《敕勒歌》、《游子吟》、《关山月》、《清平乐·六盘山》排在后六场,且《蜀道难》排在《游子吟》的前面,《沁园春·长沙》与《清平乐·六盘山》不相邻且均不排在最后,则后六场的排法有__________种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人同时参加一个外贸公司的招聘,招聘分笔试与面试两部分,先笔试后面试.甲笔试与面试通过的概率分别为0.8,0.5,乙笔试与面试通过的概率分别为0.8,0.4,且笔试通过了才能进入面试,面试通过则直接招聘录用,两人笔试与面试相互独立互不影响.
(1)求这两人至少有一人通过笔试的概率;
(2)求这两人笔试都通过却都未被录用的概率;
(3)记这两人中最终被录用的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知图形ABCDEF,内部连有线段.
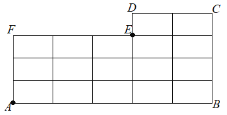
(1)由点A沿着图中的线段到达点E的最近路线有多少条?
(2)由点A沿着图中的线段到达点C的最近路线有多少条?
(3)求出图中总计有多少个矩形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com