
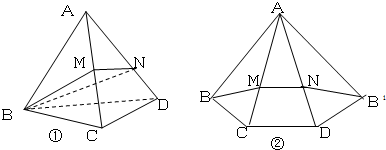
如图,已知CD是等边三角形ABC边AB上的高,沿CD将△ADC折起,使平面ADC与平面BDC互相垂直
(Ⅰ)求AB与平面BDC所成的角;
(Ⅱ)若O点在DC上,且分DC的比为![]() ,求二面角A-BO-C的正切值.
,求二面角A-BO-C的正切值.


答案:(Ⅰ)解:∵ A-DC-B为直二面角,且AD⊥DC. ∴ AD⊥平面BDC ∴ AB与平面BDC所成的角为∠ABD ∵ AD=BD,∠ADB=90° ∴ ∠ABD=45° ∴ AB与平面BDC所成的角为45°.
(Ⅱ)解:如图,过D作BO的垂线交BO于H,并延长交BC于G,连AH,AG ∵ AD⊥平面BDC,又DH⊥BO ∴ BO⊥AH(三垂线定理) ∴ ∠AHG为二面角A-BO-G的平面角 ∵ 点O在DC上,且 ∴ ∠DBO=30° ∴ BD=2DH 即 AD=2DH 在Rt△ADH中, ∴ tan∠AHG=tan(π-∠AHD)= -2 故二面角A-BO-C的正切值为-2.
|


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
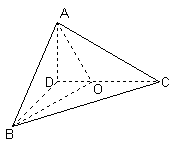
(Ⅰ)求AB与平面BDC所成的角;
(Ⅱ)若O点在DC上,且分DC的比为![]() ,求二面角A-BO-C的正切值.
,求二面角A-BO-C的正切值.

查看答案和解析>>
科目:高中数学 来源: 题型:
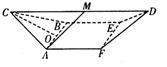
(08年长沙一中一模理)如图,已知几何体![]() 中,
中,![]() 及
及![]() 都是边长为2的等边三角形,四边形
都是边长为2的等边三角形,四边形![]() 为矩形,且
为矩形,且![]() ,
,![]() ,O为AB中点.
,O为AB中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若M为CD中点,![]() ,则当
,则当![]() 取何值时,使AM与平面ABEF所成角为
取何值时,使AM与平面ABEF所成角为![]() ?试求相应的
?试求相应的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省汕尾市陆丰市新龙中学高一(上)第二次月考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com