
【题目】某学校成立了数学、英语、音乐3个课外兴趣小组,3个小组分别有39、32、33个成员,一些成员参加了不止一个小组,具体情况如图所示.
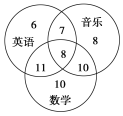
现随机选取一个成员,他属于至少2个小组的概率是________,他属于不超过2个小组的概率是________.
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 | 参赛人数 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 45 | 83 | 86 | 85 | 82 |
乙 | 45 | 83 | 84 | 85 | 133 |
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分![]() 分为优秀);
分为优秀);
③甲、乙两班成绩为85分的学生人数比成绩为其他值的学生人数多;
④乙班成绩波动比甲班小.
其中正确结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
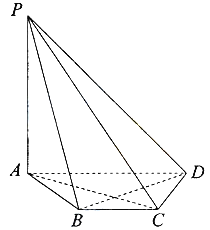
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“创文创卫”活动中,某机构为了解一小区成年居民“吸烟与性别”是否有关.从该小区中随机抽取200位成年居民,得到下边列联表:已知在全部200人中随机抽取1人,抽到不吸烟的概率为0.75.
吸烟 | 不吸烟 | 合计 | |
男 | 40 | ||
女 | 90 | ||
合计 | 200 |
(1)补充上面的列联表,并判断:能否有99.9%的把握认为“吸烟与性别”有关;
(2)用分层抽样的方法从吸烟居民中选5人出来,然后再从中抽2人出来,给小区居民谈谈吸烟的危害性,求恰好抽到“一男一女”的概率.
参考公式: 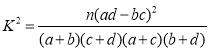 .
.
参考数据:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和为Sn,若对任意正整数n,总存在正整数m,使得Sn=am,则称数列{an}为S数列.
(1)S数列的任意一项是否可以写成其某两项的差?请说明理由.
(2)①是否存在等差数列为S数列,若存在,请举例说明;若不存在,请说明理由.
②是否存在正项递增等比数列为S数列,若存在,请举例说明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学大学毕业后,决定利用所学专业进行自主创业,经过市场调查,生产一小型电子产品需投入固定成本2万元,每生产![]() 万件,需另投入流动成本
万件,需另投入流动成本![]() 万元,当年产量小于
万元,当年产量小于![]() 万件时,
万件时,![]() (万元);当年产量不小于7万件时,
(万元);当年产量不小于7万件时,![]() (万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(万元).已知每件产品售价为6元,假若该同学生产的商品当年能全部售完.
(1)写出年利润![]() (万年)关于年产量
(万年)关于年产量![]() (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)
(2)当年产量约为多少万件时,该同学的这一产品所获年利润最大?最大年利润是多少?
(取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为![]() .
.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com