
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,其中
,其中![]() .
.
(1)求![]() 及数列
及数列![]() 的通项公式;
的通项公式;
(2)若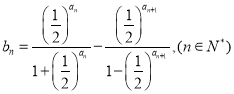 ,
,![]() 为整数,且对任意的
为整数,且对任意的![]() ,
,![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上的可导函数f (x)的导函数为![]() ,满足
,满足![]() <f (x),且f (x+2)为偶函数,f (4)=1,则不等式f (x)<ex的解集为________.
<f (x),且f (x+2)为偶函数,f (4)=1,则不等式f (x)<ex的解集为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着全民健康运动的普及,每天一万步已经成为一种健康时尚,某学校为了教职工能够健康工作,在全校范围内倡导“每天一万步”健康走活动,学校界定一人一天走路不足4千步为“健步常人”,不少于16千步为“健步超人”,其他人为“健步达人”,学校随机抽取抽查人36名教职工,其每天的走步情况统计如下:

现对抽查的36人采用分层抽样的方式选出6人,从选出的6人中随机抽取2人进行调查.
(1)求这两人健步走状况一致的概率;
(2)求“健步超人”人数![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 在一个周期内的图象如图所示,A为图象的最高点,B,C为
在一个周期内的图象如图所示,A为图象的最高点,B,C为![]() 的图象与x轴的交点,且
的图象与x轴的交点,且![]() 为等边三角形.将函数
为等边三角形.将函数![]() 的图象上各点的横坐标变为原来的
的图象上各点的横坐标变为原来的![]() 倍后,再向右平移
倍后,再向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.
的图象.

(1)求函数![]() 的解析式;
的解析式;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面ABCD为菱形,PA⊥平面ABCD,E为PD的中点.
中,底面ABCD为菱形,PA⊥平面ABCD,E为PD的中点.
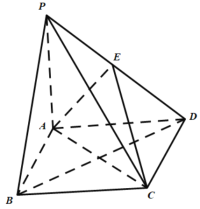
(1)求证:PB∥平面AEC;
(2)求证:平面PAC⊥平面PBD;
(3)当PA=AB=2,∠ABC=![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l经过定点P(3,5),倾斜角为
(θ为参数),直线l经过定点P(3,5),倾斜角为![]() .
.
(1)写出直线l的参数方程和曲线C的标准方程.
(2)设直线l与曲线C相交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com