已知
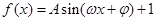
,(
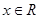
,其中
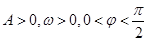
)的周期为
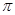
,且图像上一个最低点为
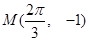
(1)求
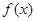
的解析式;
(2)当
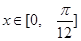
时,求
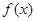
的值域.
(1)
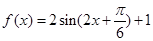
(2)
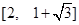
。
试题分析:(1)由
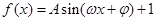
的周期为
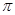
,知
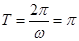
,则有
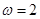
; 1分
所以
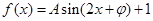
因为函数图像有一个最低点
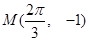
,
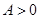
,
所以
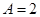
且
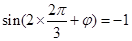
, 3分
则有
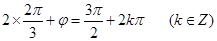
4分
解得
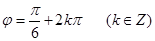
, 因为
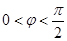
,所以
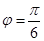
6分
所以
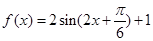
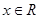
7分
(2)当
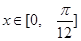
时,
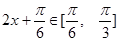
, 8分
则有
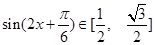
,所以
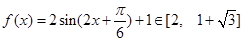
11分
即
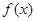
的值域为
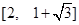
。 12分
点评:确定函数
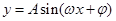
的解析式就是确定其中的参数
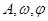
等,从图像的特征上寻找答案,它的一般步骤是:
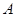
主要由最值确定,
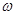
是由周期确定,周期通过特殊点观察求得,
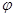
可由点在函数图像上求得,确定
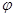
值时,注意它的不唯一性,一般要求
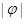
中最小的
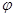
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:单选题
若函数
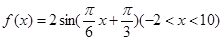
的图象与
x轴交于点A,过点A的直线
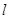
与函数的图象交于B、C两点,则
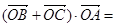
( )
A.
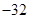
B.
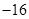
C.
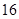
D.
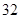
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
将
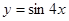
的图象向左平移
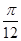
个单位,得到
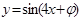
的图象,则

等于 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数

(
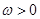
)的最小正周期为
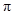
.
(1)求
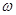
的值;
(2)求函数
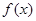
在区间
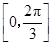
上的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
关于下列命题:①函数

在第一象限是增函数;②函数

是偶函数; ③函数

的一个对称中心是(

,0);④函数

在闭区间

上是增函数; 写出所有正确的命题的题号:
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
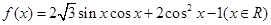
(1)求函数
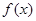
的最小正周期及在区间
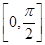
上的最大值和最小值;
(2)若
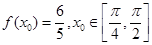
,求
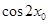
的值.
查看答案和解析>>

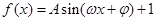 ,(
,(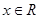 ,其中
,其中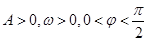 )的周期为
)的周期为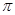 ,且图像上一个最低点为
,且图像上一个最低点为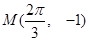
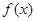 的解析式;
的解析式;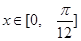 时,求
时,求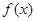 的值域.
的值域. 在第一象限是增函数;②函数
在第一象限是增函数;②函数 是偶函数; ③函数
是偶函数; ③函数 的一个对称中心是(
的一个对称中心是( ,0);④函数
,0);④函数 在闭区间
在闭区间 上是增函数; 写出所有正确的命题的题号: 。
上是增函数; 写出所有正确的命题的题号: 。