
(1) f(x)=-x3-2x+1; (2)f(x)=e1+x+2x+2.
解析:(1)用计算器或计算机作出x、f(x)的对应值表(如下表)及其图象(如图1).
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
f(x) | 34 | 13 | 4 | 1 | -2 | -11 | -32 |
由列表或图象可知,f(0)>0,f(1)<0,即f(0)·f(1)<0,说明函数f(x)在区间(0,1)内有零点,且仅有一个.故函数f(x)的零点所在大致区间为(0,1).
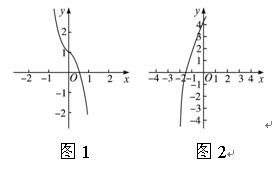
(2)易知函数f(x)=e1+x+2x+2在定义域R上是增函数.
用图形计算器或计算机作出图象,如图2.
由图象可知,f(-2)<0,f(-1)>0,即f(-2)·f(-1)<0,说明函数在区间(-2,-1)内有零点,且仅有一个.故函数f(x)的零点所在大致区间为(-2,-1).


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com