
| ¦Š |
| 3 |
| ||
| 3 |
| ¦Š |
| 4 |
| ¦Š |
| 8 |
| 3¦Š |
| 8 |
| 2 |
| ¦Š |
| 8 |
| 3 |
| ¦Š |
| 4 |
| 5¦Š |
| 6 |
| ¦Š |
| 3 |
| ¦Š |
| 3 |
| 1+a2 |
| 2¦Š |
| 3 |
| 2¦Š |
| 3 |
| 1+a2 |
| ||
| 3 |
| ¦Š |
| 4 |
| 3¦Š |
| 8 |
| ¦Š |
| 8 |
| 3¦Š |
| 8 |
| ¦Š |
| 8 |
| 2 |
| 6 |
| 2 |
| 6 |
| 2 |
| ¦Š |
| 8 |
| 2 |
| ¦Š |
| 4 |
| 2 |
| ¦Š |
| 4 |
| 5¦Š |
| 6 |
| 5¦Š |
| 6 |
| 3 |
| 5¦Š |
| 6 |
| ¦Š |
| 2 |
| ¦Š |
| 4 |



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
| ¦Š |
| 6 |
| ¦Š |
| 3 |
| 1 |
| f(x) |
| OA |
| OB |
| CO |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
|
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ2011ÄźĖÄ“ØŹ”ĆąŃō֊ѧøßæ¼ŹŹÓ¦ŠŌ¼ģ²āŹżŃ§ŹŌ¾ķ£ØĄķæĘ£©£Ø½āĪö°ę£© ĢāŠĶ£ŗĢīæÕĢā
 ”±ŹĒ”°|2y-x|”Ü2”±µÄ³ä·Ö²»±ŲŅŖĢõ¼ž£®
”±ŹĒ”°|2y-x|”Ü2”±µÄ³ä·Ö²»±ŲŅŖĢõ¼ž£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
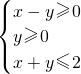 ”±ŹĒ”°|2y-x|”Ü2”±µÄ³ä·Ö²»±ŲŅŖĢõ¼ž£®
”±ŹĒ”°|2y-x|”Ü2”±µÄ³ä·Ö²»±ŲŅŖĢõ¼ž£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ2010ÄźÉ½¶«Ź”øßæ¼ŹżŃ§Ä£ÄāŹŌ¾ķ1£ØĪÄæĘ£©£Ø½āĪö°ę£© ĢāŠĶ£ŗ½ā“šĢā
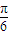 £©Ķ¼ĻóµÄŅ»øö¶Ō³ĘÖŠŠÄĪŖµć£Ø
£©Ķ¼ĻóµÄŅ»øö¶Ō³ĘÖŠŠÄĪŖµć£Ø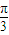 £¬0£©£»¢ŪČōŗÆŹżf£Øx£©ŌŚRÉĻĀś×ćf£Øx+1£©=
£¬0£©£»¢ŪČōŗÆŹżf£Øx£©ŌŚRÉĻĀś×ćf£Øx+1£©=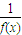 £¬Ōņf£Øx£©ŹĒÖÜĘŚĪŖ2µÄŗÆŹż£»¢ÜŌŚ”÷ABCÖŠ£¬Čō
£¬Ōņf£Øx£©ŹĒÖÜĘŚĪŖ2µÄŗÆŹż£»¢ÜŌŚ”÷ABCÖŠ£¬Čō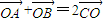 £¬ŌņS”÷ABC=S”÷BOCĘäÖŠÕżČ·ĆüĢāµÄŠņŗÅĪŖ £®
£¬ŌņS”÷ABC=S”÷BOCĘäÖŠÕżČ·ĆüĢāµÄŠņŗÅĪŖ £®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com