
【题目】AB是☉O的直径,点C是☉O上的动点(点C不与A,B重合),过动点C的直线VC垂直于☉O所在的平面,D,E分别是VA,VC的中点,则下列结论中正确的是________(填写正确结论的序号).
(1)直线DE∥平面ABC.
(2)直线DE⊥平面VBC.
(3)DE⊥VB.
(4)DE⊥AB.
科目:高中数学 来源: 题型:
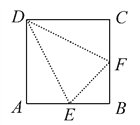
【题目】如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.
问:(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各对直线不互相垂直的是 ( )
A. l1的倾斜角为120°,l2过点P(1,0),Q(4, ![]() )
)
B. l1的斜率为-![]() ,l2过点P(1,1),Q
,l2过点P(1,1),Q![]()
C. l1的倾斜角为30°,l2过点P(3, ![]() ),Q(4,2
),Q(4,2![]() )
)
D. l1过点M(1,0),N(4,-5),l2过点P(-6,0),Q(-1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线a,b和平面M,N,且a⊥M,则下列说法正确的是 ( )
A. b∥Mb⊥a B. b⊥ab∥M
C. N⊥Ma∥N D. aNM∩N≠
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将三角形ADE沿AE折起,则下列说法正确的是________(填序号).
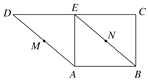
①不论D折至何位置(不在平面ABC内),都有MN∥平面DEC;②不论D折至何位置,都有MN⊥AE;③不论D折至何位置(不在平面ABC内),都有MN∥AB;④在折起过程中,一定存在某个位置,使EC⊥AD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2﹣2lnx,x∈(0,e],其中e是自然对数的底.
(1)若f(x)在x=1处取得极值,求a的值;
(2)求f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2﹣alnx(a∈R)
x2﹣alnx(a∈R)
(1)若函数f(x)在x=2处的切线方程为y=x+b,求a,b的值;
(2)讨论方程f(x)=0解的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)= ![]() ,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是 .
,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外.”其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如表 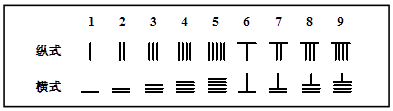
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推,例如6613用算筹表示就是: ![]() ,则9117用算筹可表示为( )
,则9117用算筹可表示为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com