
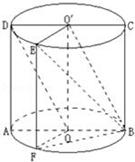
如图,圆柱的轴截面 为正方形,
为正方形,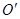 、
、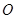 分别为上、下底面的圆心,
分别为上、下底面的圆心, 为上底面圆周上一点,已知
为上底面圆周上一点,已知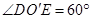 ,圆柱侧面积等于
,圆柱侧面积等于 .
.
(1)求圆柱的体积 ;
;
(2)求异面直线 与
与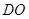 所成角
所成角 的大小.
的大小.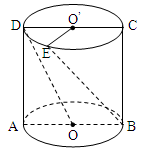
(1)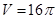 ;(2)
;(2)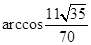 .
.
解析试题分析:(1)了解圆柱的概念,掌握圆柱体积和侧面积计算公式即能解决此题;(2)求异面直线所成角,经常采用平移法,即通过平移,将异面直线所成角转化为相交直线所成角来解决问题,此题可通过平移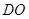 至
至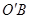 ,转化直线
,转化直线 与
与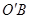 所成角来处理.
所成角来处理.
试题解析:(1)设圆柱的底面半径为 ,由题意,
,由题意, 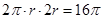
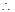
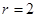 . 2分
. 2分
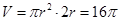 . 6分
. 6分
(2)连接 ,由于
,由于
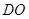 ,
,

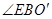 即为异面直线
即为异面直线 与
与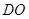 所成角 (或其补角), 8分
所成角 (或其补角), 8分
过点 作圆柱的母线交下底面于点
作圆柱的母线交下底面于点 ,连接
,连接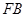 ,
,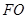
由圆柱的性质,得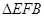 为直角三角形,四边形
为直角三角形,四边形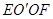 为矩形,
为矩形,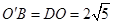 ,
,
由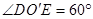 ,由等角定理,得
,由等角定理,得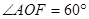 ,所以
,所以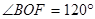 ,可解得
,可解得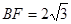 ,
,
在 中,
中,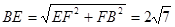 ,
,
由余弦定理,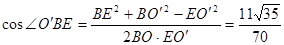 13分
13分 异面直线
异面直线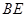 与
与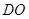 所成角
所成角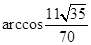 . 14分
. 14分
考点:1.圆柱的体积与表面积;2.异面直线所成角.


科目:高中数学 来源: 题型:填空题
一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的_______(填入所有可能的几何体前的编号)
①三棱锥 ②四棱锥 ③三棱柱 ④四棱柱 ⑤圆锥 ⑥圆柱
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2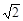 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.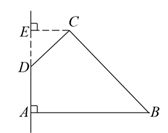
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点,△AEC面积的最小值是3.
(1)求证:AC⊥DE;
(2)求四棱锥P-ABCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com