
【题目】已知函数f(x)=cos4x﹣2sinxcosx﹣sin4x.
(1)求f(x)的最小正周期;
(2)求f(x)的单调增区间;
(3)若 ![]() ,求f(x)的值域.
,求f(x)的值域.
【答案】
(1)解:f(x)=cos4x﹣2sinxcosx﹣sin4x
=(cos2x+sin2x)(cos2x﹣sin2x)﹣sin2x
=1×(cos2x﹣sin2x)﹣sin2x
=cos2x﹣sin2x
= ![]() cos(2x+
cos(2x+ ![]() )
)
∴T= ![]() =π
=π
(2)解:∵﹣π+2kπ≤2x+ ![]() ≤2kπ,k∈Z,
≤2kπ,k∈Z,
∴﹣ ![]() π+kπ≤x≤﹣
π+kπ≤x≤﹣ ![]() +kπ,k∈Z,
+kπ,k∈Z,
∴f(x)的单调增区间为[﹣ ![]() π+kπ,﹣
π+kπ,﹣ ![]() +kπ],k∈Z
+kπ],k∈Z
(3)解:由(1)可得f(x)在[0, ![]() ]上单调递减,在[
]上单调递减,在[ ![]() ,
, ![]() ]上递增,
]上递增,
∴f(x)的最小值为﹣ ![]() ,
,
f(0)= ![]() cos(0+
cos(0+ ![]() )=1,f(
)=1,f( ![]() )=﹣1,
)=﹣1,
∴f(x)的值域为[﹣ ![]() ,1]
,1]
【解析】利用二倍角公式化成 f(x)=cos2x﹣sin2x= ![]() cos(2x+
cos(2x+ ![]() );(1)最小正周期T=π.(2)令﹣π+2kπ≤2x+
);(1)最小正周期T=π.(2)令﹣π+2kπ≤2x+ ![]() ≤2kπ,求单调递增区间,(3)根据正弦函数的性质可得f(x)在[0,
≤2kπ,求单调递增区间,(3)根据正弦函数的性质可得f(x)在[0, ![]() ]上单调递减,在[
]上单调递减,在[ ![]() ,
, ![]() ]上递增,即可求出函数的值域
]上递增,即可求出函数的值域
【考点精析】认真审题,首先需要了解正弦函数的单调性(正弦函数的单调性:在![]()
![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数).
上是减函数).


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的倾斜角为
的倾斜角为![]() 且经过点
且经过点![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,与直角坐标系
轴正半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系,设曲线
取相同的长度单位,建立极坐标系,设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围;
的取值范围;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且直线
,且直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 恒过的定点
恒过的定点![]() 的坐标;
的坐标;
(Ⅱ)在(Ⅰ)的条件下,若![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() 为
为![]() 与
与![]() 的交点,
的交点, ![]() 为
为![]() 上任意一点.
上任意一点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,并且二面角
,并且二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,关于正方体ABCD﹣A1B1C1D1 , 下面结论错误的是( ) 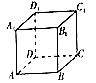
A.BD⊥平面ACC1A1
B.AC⊥BD
C.A1B∥平面CDD1C1
D.该正方体的外接球和内接球的半径之比为2:1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有4家直营店![]() ,
, ![]() ,
, ![]() ,
, ![]() ,现需将6箱货物运送至直营店进行销售,各直营店出售该货物以往所得利润统计如下表所示.根据此表,该公司获得最大总利润的运送方式有
,现需将6箱货物运送至直营店进行销售,各直营店出售该货物以往所得利润统计如下表所示.根据此表,该公司获得最大总利润的运送方式有

A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在古希腊毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形则第n个三角形数为 . 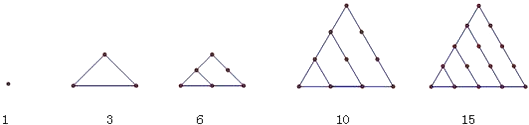
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com