
分析 (Ⅰ)由题意得$\left\{\begin{array}{l}{a=2}\\{\frac{c}{a}=\frac{1}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,求出b,由此能求出椭圆C的方程;
(Ⅱ)设A(x1,y1),B(x2,y2),Q(x3,y3),求出p点的坐标,由B,Q,P三点共线,得$\overrightarrow{BP}=λ\overrightarrow{BQ}$,联立方程组求解得x3,y3,再结合已知条件能求出λ值,则$\frac{|BP|}{|BQ|}$的值可求.
解答 解:(Ⅰ)由题意得$\left\{\begin{array}{l}{a=2}\\{\frac{c}{a}=\frac{1}{2}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,
解得$b=\sqrt{3}$.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)设A(x1,y1),B(x2,y2),Q(x3,y3),
∵点P在直线AO上且满足|PO|=3|OA|,
∴P(3x1,3y1).
∵B,Q,P三点共线,
∴$\overrightarrow{BP}=λ\overrightarrow{BQ}$.
∴(3x1-x2,3y1-y2)=λ(x3-x2,y3-y2),
即$\left\{\begin{array}{l}{3{x}_{1}-{x}_{2}=λ({x}_{3}-{x}_{2})}\\{3{y}_{1}-{y}_{2}=λ({y}_{3}-{y}_{2})}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{3}=\frac{3}{λ}{x}_{1}+\frac{λ-1}{λ}{x}_{2}}\\{{y}_{3}=\frac{3}{λ}{y}_{1}+\frac{λ-1}{λ}{y}_{2}}\end{array}\right.$,
∵点Q在椭圆C上,∴$\frac{{{x}_{3}}^{2}}{4}+\frac{{{y}_{3}}^{2}}{3}=1$.
∴$\frac{(\frac{3}{λ}{x}_{1}+\frac{λ-1}{λ}{x}_{2})^{2}}{4}+\frac{(\frac{3}{λ}{y}_{1}+\frac{λ-1}{λ}{y}_{2})^{2}}{3}=1$.
即$\frac{9}{{λ}^{2}}(\frac{{{x}_{1}}^{2}}{4}+\frac{{{y}_{1}}^{2}}{3})+(\frac{λ-1}{λ})^{2}(\frac{{{x}_{2}}^{2}}{4}+\frac{{{y}_{2}}^{2}}{3})$$-\frac{6(λ-1)}{{λ}^{2}}(\frac{{x}_{1}{x}_{2}}{4}+\frac{{y}_{1}{y}_{2}}{3})=1$,
∵A,B在椭圆C上,
∴$\frac{{{x}_{1}}^{2}}{4}+\frac{{{y}_{1}}^{2}}{3}=1$,$\frac{{{x}_{2}}^{2}}{4}+\frac{{{y}_{2}}^{2}}{3}=1$.
∵直线OA,OB的斜率之积为$-\frac{3}{4}$,
∴$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}=-\frac{3}{4}$,即$\frac{{x}_{1}{x}_{2}}{4}+\frac{{y}_{1}{y}_{2}}{3}=0$.
∴$\frac{9}{{λ}^{2}}+(\frac{λ-1}{λ})^{2}=1$,解得λ=5.
∴$\frac{|BP|}{|BQ|}$=|λ|=5.
点评 本题考查椭圆的标准方程,考查直线与椭圆位置关系的应用,训练了向量法在求解圆锥曲线问题中的应用,考查运算能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
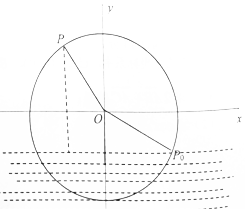 一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y+4)2=2 | B. | (x+1)2+(y-4)2=2 | C. | (x-1)2+(y-4)2=2 | D. | (x+1)2+(y+4)2=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 130万元 | B. | 130.25万元 | C. | 120万元 | D. | 100万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com