
【题目】如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.若在通道的分叉处,小弹子以相同的概率落入每个通道,记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).某研究性学习小组经探究发现小弹子落入第n层的第m个通道的次数服从二项分布,请你解决下列问题.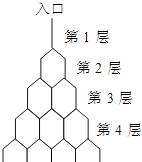
(1)求P(2,1),P(3,2)及P(4,2)的值,并猜想P(n,m)的表达式.(不必证明)
(2)设小弹子落入第6层第m个竖直通道得到分数为ξ,其中ξ= ![]() ,试求ξ的分布列及数学期望.
,试求ξ的分布列及数学期望.
【答案】
(1)解:根据已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是 ![]() ,小球遇到第n行第m个障碍物(从左至右)上顶点的概率为P(n,m),可得
,小球遇到第n行第m个障碍物(从左至右)上顶点的概率为P(n,m),可得
P(2,1)= ![]() ,P(3,2)=
,P(3,2)= ![]() =
= ![]() ,P(4,2)=
,P(4,2)= ![]() =
= ![]()
猜想P(n,m)= ![]() ;
;
(2)解:ξ的可能取值为3,2,1,
P(ξ=3)=P(6,1)+P(6,6)= ![]() ,
,
P(ξ=2)=P(6,2)+P(6,5)= ![]() =
= ![]() ,
,
P(ξ=1)=P(6,3)+P(6,4)= ![]()
分布列为:
ξ | 3 | 2 | 1 |
P |
|
|
|
Eξ=3× ![]() +2×
+2× ![]() +1×
+1× ![]() =
= ![]() .
.
【解析】(1)根据小弹子以相同的概率落入每个通道,在每一个分叉处小球落入那一个通道的概率是相同的,根据独立重复试验的概率公式得到结果,推出具有一般性的结论.(2)根据题意知变量ξ的可能取值是3,2,1,结合变量对应的事件和前一问做出的概率公式,写出变量对应的概率和分布列,求出期望值.
【考点精析】利用离散型随机变量及其分布列对题目进行判断即可得到答案,需要熟知在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


科目:高中数学 来源: 题型:
【题目】关于函数f(x)=﹣tan2x,有下列说法: ①f(x)的定义域是{x∈R|x≠ ![]() +kπ,k∈Z}②f(x)是奇函数 ③在定义域上是增函数 ④在每一个区间(﹣
+kπ,k∈Z}②f(x)是奇函数 ③在定义域上是增函数 ④在每一个区间(﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() )(k∈Z)上是减函数 ⑤最小正周期是π其中正确的是( )
)(k∈Z)上是减函数 ⑤最小正周期是π其中正确的是( )
A.①②③
B.②④⑤
C.②④
D.③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛中获胜的事件是独立的,并且获胜的概率均为 ![]() .
.
(1)求这支篮球队首次获胜前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好获胜3场的概率;
(3)求这支篮球队在6场比赛中获胜场数的期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S﹣ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD. 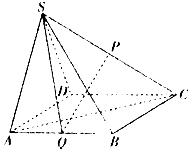
(1)求证:PQ∥平面SAD;
(2)求证:SQ⊥AC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:
①若f(x)=x3+(a﹣1)x2+3x+1没有极值点,则﹣2<a<4;
②集合M={1,2,zi},i为虚数单位,N={3,4},M∩N={4},则复数z=﹣4i;
③若函数f(x)= ![]() ﹣m有两个零点,则m<
﹣m有两个零点,则m< ![]() .
.
其中正确的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为D,若满足①f(x)在D内是单调函数,②存在[m,n]D,使f(x)在[m,n]上的值域为 ![]() ,那么就称y=f(x)为“好函数”.现有f(x)=loga(ax+k),(a>0,a≠1)是“好函数”,则k的取值范围是( )
,那么就称y=f(x)为“好函数”.现有f(x)=loga(ax+k),(a>0,a≠1)是“好函数”,则k的取值范围是( )
A.(0,+∞)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com