
【题目】已知函数![]() 其中
其中![]() ,
,![]() 为常数且
为常数且![]() 在
在![]() 处取得极值.
处取得极值.
![]() 1
1![]() 当
当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
![]() 2
2![]() 若
若![]() 在
在![]() 上的最大值为1,求
上的最大值为1,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() 或
或![]()
【解析】
![]() 由函数的解析式,可求出函数导函数的解析式,进而根据
由函数的解析式,可求出函数导函数的解析式,进而根据![]() 是
是![]() 的一个极值点
的一个极值点![]() ,可构造关于a,b的方程,根据
,可构造关于a,b的方程,根据![]() 求出b值;可得函数导函数的解析式,分析导函数值大于0和小于0时,x的范围,可得函数
求出b值;可得函数导函数的解析式,分析导函数值大于0和小于0时,x的范围,可得函数![]() 的单调区间;
的单调区间;![]() 对函数求导,写出函数的导函数等于0的x的值,列表表示出在各个区间上的导函数和函数的情况,求出极值,把极值同端点处的值进行比较得到最大值,最后利用条件建立关于a的方程求得结果.
对函数求导,写出函数的导函数等于0的x的值,列表表示出在各个区间上的导函数和函数的情况,求出极值,把极值同端点处的值进行比较得到最大值,最后利用条件建立关于a的方程求得结果.
![]() 因为
因为![]() 所以
所以![]() ,
,
因为函数![]() 在
在![]() 处取得极值,
处取得极值,
![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,![]() 随x的变化情况如下表:
随x的变化情况如下表:
x |
|
|
| 1 |
|
|
| 0 |
| 0 |
|
| 增 | 极大值 | 减 | 极小值 | 增 |
所以![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]()
![]() 因为
因为![]()
令![]() ,
,![]() ,
,![]()
因为![]() 在
在![]() 处取得极值,所以
处取得极值,所以![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,
令![]() ,解得
,解得![]()
当![]() ,
,![]()
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增
上单调递增
所以最大值1可能在![]() 或
或![]() 处取得
处取得
而![]()
所以![]() ,解得
,解得![]()
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,![]() 上单调递增
上单调递增
所以最大值1可能在![]() 或
或![]() 处取得
处取得
而![]() ,
,
所以![]() ,
,
解得![]() ,与
,与![]() 矛盾.
矛盾.
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,在
上单调递增,在![]() 单调递减,
单调递减,
所以最大值1可能在![]() 处取得,而
处取得,而![]() ,矛盾。
,矛盾。
综上所述,![]() 或
或![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线
轴正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,直线![]() 的参数方程为
的参数方程为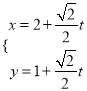 (
(![]() 为参数),圆
为参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() 两点,若点
两点,若点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某些商家为消费者提供免费塑料袋,使购物消费更加方便快捷,但是我们更应关注它对环境的潜在危害.为了解某市所有家庭每年丢弃塑料袋个数的情况,统计人员采用了科学的方法,随机抽取了200户,对他们某日丢弃塑料袋的个数进行了统计,结果如下表:

(1)求当日这200户家庭平均每户丢弃塑料袋的个数;
(2)假设某市现有家庭100万户,据此估计全市所有家庭每年(以365天计算)丟弃塑料袋的总数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个人独立地破译一个密码,他们能译出密码的概率分别为![]() 和
和![]() .
.
(1)求2个人都译出密码的概率;
(2)求2个人都译不出密码的概率;
(3)求至多1个人都译出密码的概率;
(4)求至少1个人都译出密码的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.

(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下表格.
(i)请将表格补充完整;
短潜伏者 | 长潜伏者 | 合计 | |
60岁及以上 | 90 | ||
60岁以下 | 140 | ||
合计 | 300 |
(ii)研究发现,某药物对新冠病毒有一定的抑制作用,现需在样本中60岁以下的140名患者中按分层抽样方法抽取7人做I期临床试验,再从选取的7人中随机抽取两人做Ⅱ期临床试验,求两人中恰有1人为“长潜伏者”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对边分别为a、b、c,且2acosC=2b-c.
(1)求角A的大小;
(2)若AB=3,AC边上的中线SD的长为![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将所有的正奇数按以下规律分组,第一组:1;第二组:3,5,7;第三组:9,11,13,15,17;…![]() 表示n是第i组的第j个数,例如
表示n是第i组的第j个数,例如![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com