分析:(1)法一:由于λ不确定,从而E点是个动点,而要A
1C⊥平面BED,所以不妨考虑A
1C⊥平面BED满足的条件,从而发现必须有A
1C⊥BE,由三垂线定理,得到B
1C⊥BE,由三角形相似容易得到λ的值,
法二:用向量法,以D为坐标原点,射线DA为x轴的正半轴,射线DC为y轴的正半轴,射线DD
1为z轴的正半轴,建立如图所示直角坐标系D-xyz.则:D(0,0,0),B(2,2,0),C(0,2,0),A
1(2,0,4),由于CE=λCC
1,而CC
1的坐标可求,A
1C坐标可求,若A
1C⊥平面BED,则A
1C⊥DE,由向量内积定义可求λ的值;
(2)法一:在解决问题(1)的基础上,可以作出二面角的平面角,通过解三角形解决.
法二:用向量法,由(1)知平面BDE的一个法向量为
=(-2,2,-4),故只需求平面DA
1B的一个法向量,设为n=(x,y,z),则n⊥
,n⊥
,通过内积为0求之,再计算向量n与向量A
1C的夹角即可.
解答:解:法一:(1)连接B
1C交BE于点F,连接AC交BD于点G,
∴AC⊥BD,由垂直关系得,A
1C⊥BD,
若A
1C⊥平面BED,则A
1C⊥BE,
由垂直关系可得B
1C⊥BE,
∴△BCE∽△B
1BC,∴
=
=
,
∴CE=1,∴λ=
=
.
(2)连接A
1G,连接EG交A
1C于H,则A
1G⊥BD.
∵A
1C⊥平面BED,
∴∠A
1GE是二面角A
1-BD-E的平面角.
∵A
1G=3
,EG=
,A
1E=
,
∴cos∠A
1GE=
=
,
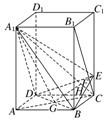
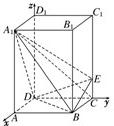
法二:(1)以D为坐标原点,射线DA为x轴的正半轴,射线DC为y轴的正半轴,射线DD
1为z轴的正半轴,建立如图所示直角坐标系D-xyz.
依题设,D(0,0,0),B(2,2,0),C(0,2,0),A
1(2,0,4),
∵CE=λCC
1=4λ,∴E(0,2,4λ),
∴
=(2,2,0),
=(2,0,4),
=(-2,2,-4),
=(0,2,4λ),
∵
•
=2×(-2)+2×2+0×(-4)=0,
∴
⊥
,∴DB⊥A
1C.
若A
1C⊥平面BED,则A
1C⊥DE,∴
⊥
,
∴
•
=(-2)×0+2×2+(-4)×4λ=4-16λ=0,
∴λ=
.
(2)设向量n=(x,y,z)是平面DA
1B的一个法向量,
则n⊥
,n⊥
,∴2x+2y=0,2x+4z=0,
令z=1,则x=-2,y=2,∴n=(-2,2,1)
由(1)知平面BDE的一个法向量为
=(-2,2,-4)
∴cos<n,
>=
=
.
即二面角A
1-BD-E的余弦值为
.
点评:本题考查直线垂直于平面、二面角的求法,在长方体、正方体等较为规则的几何体中,因为容易建立空间坐标系,可以考虑向量法解决,也可以用几何法推导,但是一定要注意问题中有连续的几问时,前一问对后面问题的影响,从而使后面的问题的解决变得简捷.

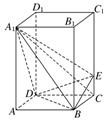 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上,且CE=λCC1.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上,且CE=λCC1.



 名校课堂系列答案
名校课堂系列答案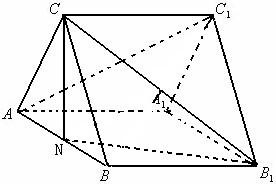 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
