
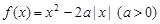 .
.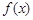 的奇偶性,并写出
的奇偶性,并写出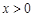 时
时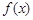 的单调增区间;
的单调增区间;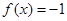 有解,求实数
有解,求实数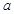 的取值范围.
的取值范围. 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源:不详 题型:解答题
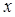 (百万元)与销售额
(百万元)与销售额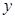 (百万元)之间有如下对应数据:
(百万元)之间有如下对应数据: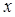 | 2 | 4 | 5 | 6 | 8 |
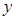 | 30 | 40 | 50 | 60 | 70 |
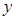 与
与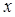 之间具有线性相关关系.
之间具有线性相关关系.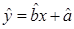 ;
;
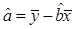 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 层,总开发费用为
层,总开发费用为 万元,求函数
万元,求函数 的表达式(总开发费用=总建筑费用+购地费用);
的表达式(总开发费用=总建筑费用+购地费用);查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
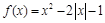 的图像,并写出该函数的单调区间与值域。
的图像,并写出该函数的单调区间与值域。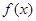 的解析式写成分段函数;
的解析式写成分段函数;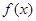 的图象,并根据图象写出函数
的图象,并根据图象写出函数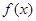 的单调区间和值域.
的单调区间和值域.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 方案 | 类别 | 基本费用 | 超时费用 |
| 甲 | 包月制(不限时) | 100元 | 无 |
| 乙 | 有限包月制(限60小时) | 60元 | 3元/小时(无上限) |
| 丙 | 有限包月制(限30小时) | 40元 | 3元/小时(无上限) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
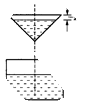

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com