
【题目】设数列{an}满足:①a1=1;②所有项an∈N*;③1=a1<a2<…<an<an+1<….设集合Am={n|an≤m,m∈N*),将集合Am中的元素的最大值记为bm,即bm是数列{an}中满足不等式an≤m的所有项的项数的最大值.我们称数列{bn}为数列{an}的伴随数列.
例如,数列1,3,5的伴随数列为1,1,2,2,3.
(I)若数列{an}的伴随数列为1,1,2,2,2,3,3,3,3……,请写出数列{an};
(II)设an=4n-1,求数列{an}的伴随数列{bn}的前50项之和;
(III)若数列{an}的前n项和![]() (其中c为常数),求数列{an}的伴随数列{bm}的前m项和Tm.
(其中c为常数),求数列{an}的伴随数列{bm}的前m项和Tm.
【答案】(I)1,3,6 (II)Tm=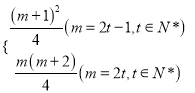
【解析】试题分析:(1)直接根据伴随数列的定义可得出数列![]() 的前三项;(2)当
的前三项;(2)当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() 当
当![]() 时,
时, ![]()
![]() ,(3)讨论两种情况,当
,(3)讨论两种情况,当![]() 时;
时; ![]() ;当
;当![]() 时,
时, ![]() .
.
试题解析:(I)1,3,6 (II)由an=4n-1≤m,得n≤l+log4m(m∈N*)
当1≤m≤3,m∈N*时,b1=b2=b3=1
当4≤m≤15,m∈N*时,b4=b5=…=b15=2
当16≤m≤50,m∈N*时,b16=b17=…=b50=3
∴b1+b2+…+b50=1×3+2×12+3×35=132
(III)∵a1=S1=1+c=1 ∴c=0
当n≥2时,an=Sn-Sn-1=2n-1 ∴an=2n-1(n∈N*)
由an=2n-l≤m得,n≤![]() (m∈N*)
(m∈N*)
因为使得an≤m成立的n的最大值为bm,
所以b1=b2=1,b3=b4=2,…,b2t-1=b2t=t(t∈N*)
当m=2t-1(t∈N*)时;
Tm=2·![]() ·(t-1)+t=t2=
·(t-1)+t=t2=![]() (m+1)2
(m+1)2
当m=2t (t∈N*)时;
Tm=2·![]() ·t=t2+t=
·t=t2+t=![]() m(m+2)
m(m+2)
所以Tm=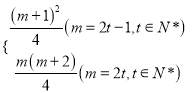


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】![]() 汉字听写大会
汉字听写大会![]() 不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试
不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试![]() 现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组
现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,
,![]() ,第6组
,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

![]() 若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
![]() 试估计该市市民正确书写汉字的个数的平均数与中位数;
试估计该市市民正确书写汉字的个数的平均数与中位数;
![]() 已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市民组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2012年的自主招生考试成绩中随机抽取![]() 名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
名中学生的笔试成绩,按成绩分组,得到的频率分布表如表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| ① |
|
第3组 |
| 30 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|

(1)请先求出频率分布表中![]() 位置的相应数据,再完成频率分布直方图;
位置的相应数据,再完成频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第![]() 组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
组中用分层抽样抽取名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试;
(3)在(2)的前提下,学校决定在![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生接受
名学生接受![]() 考官进行面试,求:第
考官进行面试,求:第![]() 组至少有一名学生被考官
组至少有一名学生被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在杨辉三角形中,从第2行开始,除1以外,其它每一个数值是它上面的两个数值之和,该三角形数阵开头几行如图所示.

(1)在杨辉三角形中是否存在某一行,使该行中三个相邻的数之比是3∶4∶5?若存在,试求出是第几行;若不存在,请说明理由;
(2)已知n,r为正整数,且n≥r+3.求证:任何四个相邻的组合数C,C![]() ,C
,C![]() ,C
,C![]() 不能构成等差数列.
不能构成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度![]() (单位:
(单位:![]() ),对某种鸡的时段产蛋量
),对某种鸡的时段产蛋量![]() (单位:
(单位:![]() ) 和时段投入成本
) 和时段投入成本![]() (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度![]() 和产蛋量
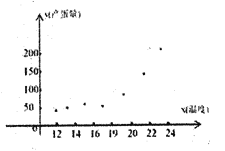
和产蛋量![]() 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
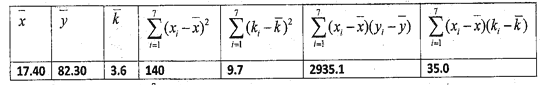
其中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量![]() 关于鸡舍时段控制温度
关于鸡舍时段控制温度![]() 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)
(2)若用![]() 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知时段投入成本![]() 与
与![]() 的关系为
的关系为![]() ,当时段控制温度为
,当时段控制温度为![]() 时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有线性相关关系的数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为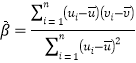 ,
,![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】合肥一中、六中为了加强交流,增进友谊,两校准备举行一场足球赛,由合肥一中版画社的同学设计一幅矩形宣传画,要求画面面积为![]() ,画面的上、下各留
,画面的上、下各留![]() 空白,左、右各留
空白,左、右各留![]() 空白.
空白.

(1)如何设计画面的高与宽的尺寸,才能使宣传画所用纸张面积最小?
(2)设画面的高与宽的比为![]() ,且
,且![]() ,求
,求![]() 为何值时,宣传画所用纸张面积最小?
为何值时,宣传画所用纸张面积最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com