
【题目】如图,在直角梯形ABCD中,AB⊥AD,AB∥DC,AB=2,AD=DC=1,图中圆弧所在圆的圆心为点C,半径为 ![]() ,且点P在图中阴影部分(包括边界)运动.若
,且点P在图中阴影部分(包括边界)运动.若 ![]() =x
=x ![]() +y
+y ![]() ,其中x,y∈R,则4x﹣y的取值范围是( )
,其中x,y∈R,则4x﹣y的取值范围是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:以A为坐标原点,AB为x轴,DA为y轴建立平面直角坐标系则A(0,0),D(0,1),C(1,1),B(2,0) 直线BD的方程为x+2y﹣2=0,C到BD的距离d= ![]() ;
;
∴以点C为圆心,以 ![]() 为半径的圆方程为(x﹣1)2+(y﹣1)2=
为半径的圆方程为(x﹣1)2+(y﹣1)2= ![]() ,
,
设P(m,n)则 ![]() =(m,n),
=(m,n), ![]() =(2,0),
=(2,0), ![]() =(﹣1,1);
=(﹣1,1);
∴(m,n)=(2x﹣y,y)
∴m=2x﹣y,n=y,
∵P在圆内或圆上
∴(2x﹣y﹣1)2+(y﹣1)2≤ ![]() ,
,
设4x﹣y=t,则y=4x﹣t,代入上式整理得
80x2﹣(48t+32)x+8t2+7≤0,
设f(x)=80x2﹣(48t+32)x+8t2+7,x∈[ ![]() ,
, ![]() ],
],
则 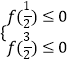 ,
,
解得2≤t≤3+ ![]() ,
,
∴4x﹣y的取值范围是[2,3+ ![]() ].
].
故选:B.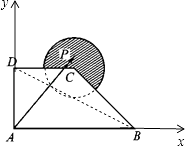


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】为了引导居民合理用水,某市决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) | (0,10] | (10,15] | (15,+∞) |
从本市随机抽取了10户家庭,统计了同一个月的用水量,得到如图所示的茎叶图.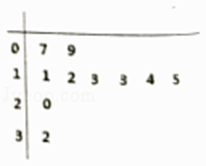
(1)现要在这10户家庭中任意选取3户,求取到第二阶梯水量的户数的分布列和均值;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到n户月用水量为第二阶梯水量的可能性最大,求出n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( )
A.(2,+∞)
B.(1,+∞)
C.(-∞,-2)
D.(-∞,-1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 (本小题满分12分)
已知圆C:![]() ,直线
,直线![]() 过定点A (1,0).
过定点A (1,0).
(1)若![]() 与圆C相切,求
与圆C相切,求![]() 的方程;
的方程;
(2)若![]() 与圆C相交于P、Q两点,求三角形CPQ的面积的最大值,并求此时直线
与圆C相交于P、Q两点,求三角形CPQ的面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 中,若对任意
中,若对任意![]() 都有
都有![]() (
(![]() 为常数)成立,则称
为常数)成立,则称![]() 为“等差比数列”,下面对“等差比数列” 的判断:①
为“等差比数列”,下面对“等差比数列” 的判断:①![]() 不可能为
不可能为![]() ;②等差数列一定是等差比数列; ③等比数列一定是等差比数列 ;④通项公式为
;②等差数列一定是等差比数列; ③等比数列一定是等差比数列 ;④通项公式为![]() (其中
(其中![]() ,且
,且![]() ,
,![]() )的数列一定是等差比数列,其中正确的判断是( )
)的数列一定是等差比数列,其中正确的判断是( )
A. ①③④ B. ②③④ C. ①④ D. ①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+1)+ax,其中a∈R.
(Ⅰ) 当a=﹣1时,求证:f(x)≤0;
(Ⅱ) 对任意x2≥ex1>0,存在x∈(﹣1,+∞),使 ![]() 成立,求a的取值范围.(其中e是自然对数的底数,e=2.71828…)
成立,求a的取值范围.(其中e是自然对数的底数,e=2.71828…)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com