
【题目】判断下列函数的奇偶性:
(1)f(x)=x+1;
(2)f(x)=x3+3x,x∈[-4,4);
(3)f(x)=|x-2|-|x+2|;
(4)f(x)=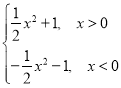
【答案】(1)既不是奇函数又不是偶函数;(2)既不是奇函数又不是偶函数;(3)奇函数;(4)奇函数.
【解析】
根据函数的奇偶性的定义,结合函数的解析式,逐个判定,即可求解.
(1)函数f(x)=x+1的定义域为实数集R,关于原点对称.
因为f(-x)=-x+1=-(x-1),-f(x)=-(x+1),即f(-x)≠-f(x),f(-x)≠f(x),
所以函数f(x)=x+1既不是奇函数又不是偶函数.
(2)因为函数的定义域不关于原点对称,即存在-4∈[-4,4),而4[-4,4),
所以函数f(x)=x3+3x,x∈[-4,4)既不是奇函数又不是偶函数.
(3)函数f(x)=|x-2|-|x+2|的定义域为实数集R,关于原点对称.
因为f(-x)=|-x-2|-|-x+2|=|x+2|-|x-2|=-(|x-2|-|x+2|)=-f(x),
所以函数f(x)=|x-2|-|x+2|是奇函数.
(4)函数的定义域为(-∞,0)∪(0,+∞),关于原点对称.
当x>0时,-x<0,f(-x)=-![]() (-x)2-1=-(
(-x)2-1=-(![]() x2+1)=-f(x);
x2+1)=-f(x);
当x<0时,-x>0,f(-x)=![]() (-x)2+1=
(-x)2+1=![]() x2+1=-(-
x2+1=-(-![]() x2-1)=-f(x).
x2-1)=-f(x).
综上可知,函数f(x)=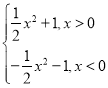 是奇函数.
是奇函数.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() (a>0,b>0)的右焦点为
(a>0,b>0)的右焦点为![]() ,右顶点为A,过F作
,右顶点为A,过F作![]() 的垂线与双曲线交于
的垂线与双曲线交于![]() 、
、![]() 两点,过
两点,过![]() 分别作
分别作![]() 的垂线,两垂线交于点
的垂线,两垂线交于点![]() ,若
,若![]() 到直线
到直线![]() 的距离小于
的距离小于![]() , 则双曲线的渐近线斜率的取值范围是
, 则双曲线的渐近线斜率的取值范围是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是某市环保局连续30天对空气质量指数的监测数据:
61 76 70 56 81 91 55 91 75 81
88 67 101 103 57 91 77 86 81 83
82 82 64 79 86 85 75 71 49 45
(1)完成下面的频率分布表;
(2)完成下面的频率分布直方图,并写出频率分布直方图中![]() 的值;
的值;
(3)在本月空气质量指数大于等于91的这些天中随机选取两天,求这两天中至少有一天空气质量指数在区间![]() 内的概率.
内的概率.
分组 | 频数 | 频率 |
[41,51) | 2 |
|
[51,61) | 3 |
|
[61,71) | 4 |
|
[71,81) | 6 |
|
[81,91) | ||
[91,101) | 3 | |
[101,111) |
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前某地区有100万人,经过x年后为y万人,如果年平均增长率是1.2%,请回答下列问题:
(1)试推算出y关于x的函数关系式;
(2)计算10年后该地区的人口总数(精确到0.1万人);
(3)计算大约多少年后该地区的人口总数会达到120万(精确到1年).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知直线
中,已知直线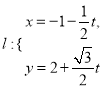 (
(![]() 为参数),曲线
为参数),曲线![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系.
轴的正半轴为极轴建立坐标系.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的极坐标方程;
的极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x-b|的最小值为1.
(1)证明:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列函数的奇偶性:
(1)f(x)=x+1;
(2)f(x)=x3+3x,x∈[-4,4);
(3)f(x)=|x-2|-|x+2|;
(4)f(x)=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋中装有大小相同的2个白球、2个红球和1个黄球.一项游戏规定:每个白球、红球和黄球的分值分别是0分、1分和2分,每一局从袋中一次性取出三个球,将3个球对应的分值相加后称为该局的得分,计算完得分后将球放回袋中.当出现第![]() 局得
局得![]() 分(
分(![]() )的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
)的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
(1)求在一局游戏中得3分的概率;
(2)求游戏结束时局数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则![]() ;
;
②若C为双曲线,则![]() 或
或![]() ;
;
③曲线C不可能是圆;
④若![]() ,曲线C为椭圆,且焦点坐标为
,曲线C为椭圆,且焦点坐标为![]() ;
;
⑤若![]() ,曲线C为双曲线,且虚半轴长为
,曲线C为双曲线,且虚半轴长为![]() .
.
其中真命题的序号为____________.(把所有正确命题的序号都填在横线上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com