
【题目】在直角坐标系xOy中,曲线C1的参数方程是 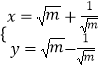 (m为参数),直线l交曲线C1于A,B两点;以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=4sin(θ﹣
(m为参数),直线l交曲线C1于A,B两点;以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=4sin(θ﹣ ![]() ),点P(ρ,
),点P(ρ, ![]() )在曲线C2上.
)在曲线C2上.
(1)求曲线C1的普通方程及点P的直角坐标;
(2)若直线l的倾斜角为 ![]() 且经过点P,求|PA|+|PB|的值.
且经过点P,求|PA|+|PB|的值.
科目:高中数学 来源: 题型:
【题目】设公比不为1的等比数列{an}的前n项和Sn , 已知a1a2a3=8,S2n=3(a1+a3+a5+…+a2n﹣1)(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=(﹣1)nlog2an , 求数列{bn}的前2017项和T2017 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=a(x﹣1)2﹣xe2﹣x .
(Ⅰ)若曲线y=f(x)在点(2,f(2))处的切线与x轴平行,求a的值;
(Ⅱ)若 ![]() ,求f(x)的单调区间.
,求f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,A,B分别为椭圆C的左、右顶点,F为右焦点.直线y=6x与C的交点到y轴的距离为
,A,B分别为椭圆C的左、右顶点,F为右焦点.直线y=6x与C的交点到y轴的距离为 ![]() ,过点B作x轴的垂线l,D为l 上异于点B的一点,以BD为直径作圆E.
,过点B作x轴的垂线l,D为l 上异于点B的一点,以BD为直径作圆E.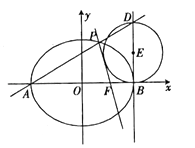
(1)求C 的方程;
(2)若直线AD与C的另一个交点为P,证明PF与圆E相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若sinA=cos( ![]() ﹣B),a=3,c=2.
﹣B),a=3,c=2.
(1)求 ![]() 的值;
的值;
(2)求tan( ![]() ﹣B)的值.
﹣B)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某饮料生产企业为了占有更多的市场份额,拟在2017年度进行一系列促销活动,经过市场调查和测算,饮料的年销售量x万件与年促销费t万元间满足 ![]() .已知2017年生产饮料的设备折旧,维修等固定费用为3万元,每生产1万件饮料需再投入32万元的生产费用,若将每件饮料的售价定为其生产成本的150%与平均每件促销费的一半之和,则该年生产的饮料正好能销售完.
.已知2017年生产饮料的设备折旧,维修等固定费用为3万元,每生产1万件饮料需再投入32万元的生产费用,若将每件饮料的售价定为其生产成本的150%与平均每件促销费的一半之和,则该年生产的饮料正好能销售完.
(1)将2017年的利润y(万元)表示为促销费t(万元)的函数;
(2)该企业2017年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入-生产成本-促销费,生产成本=固定费用+生产费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,曲线
中,曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),在以
为参数),在以 ![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 ![]() 是圆心为
是圆心为 ![]() ,半径为1的圆.
,半径为1的圆.
(1)求曲线 ![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)设 ![]() 为曲线
为曲线 ![]() 上的点,
上的点, ![]() 为曲线
为曲线 ![]() 上的点,求
上的点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com