【答案】
分析:(1)当n=1时,S
1=b
1,
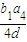
=
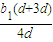
=b
1,原式成立.假设当n=k时,S
k=
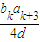
成立,由此证明n=k+1时,等式仍然成立.
(2)由3a
5=8a
12>0,知3a
5=8(a
5+7d),a
5=-
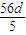
>0,所以d<0.由a
16=a
5+11d=-
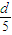
>0,a
17=a
5+12d=
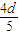
<0,知a
1>a
2>a
3>…>a
16>0>a
17>a
18,b
1>b
2>b
3>…>b
14>0>b
17>b
18,由此能够推导出S
n中S
16最大.
解答:解:(1)证明:当n=1时,S
1=b
1,
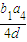
=
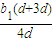
=b
1,原式成立.(1分)
假设当n=k时,S
k=
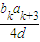
成立,(2分)
则S
k+1=S
k+b
k+1=
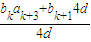
(4分)
=
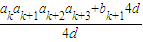
=
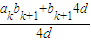
=
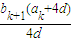
=
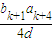
(6分)
所以n=k+1时,等式仍然成立,故对于任意n∈N*,都有S
n=
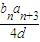
;(8分)
(2)因为3a
5=8a
12>0,所以3a
5=8(a
5+7d),a
5=-
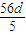
>0,所以d<0
又a
16=a
5+11d=-
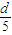
>0,a
17=a
5+12d=

<0,(11分)
所以a
1>a
2>a
3>…>a
16>0>a
17>a
18,b
1>b
2>b
3>…>b
14>0>b
17>b
18,
因为b
15=a
15a
16a
17<0,b
16=a
16a
17a
18>0,(13分)
a
15=a
5+10d=-
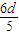
>0,a
18=a
5+13d=
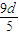
<0,
所以a
15<-a
18,所以b
15>-b
16,b
15+b
16>0,(15分)
故S
16>S
14,所以S
n中S
16最大.(16分)
点评:本题考查数列和函数的综合运用,解题时要认真审题,注意数列归纳法的合理运用,恰当地进行等价转化.

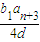 ;
;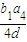 =
=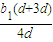 =b1,原式成立.假设当n=k时,Sk=
=b1,原式成立.假设当n=k时,Sk=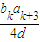 成立,由此证明n=k+1时,等式仍然成立.
成立,由此证明n=k+1时,等式仍然成立.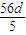 >0,所以d<0.由a16=a5+11d=-
>0,所以d<0.由a16=a5+11d=-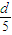 >0,a17=a5+12d=
>0,a17=a5+12d=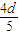 <0,知a1>a2>a3>…>a16>0>a17>a18,b1>b2>b3>…>b14>0>b17>b18,由此能够推导出Sn中S16最大.
<0,知a1>a2>a3>…>a16>0>a17>a18,b1>b2>b3>…>b14>0>b17>b18,由此能够推导出Sn中S16最大.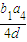 =
=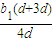 =b1,原式成立.(1分)
=b1,原式成立.(1分)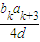 成立,(2分)
成立,(2分)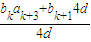 (4分)
(4分)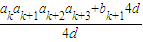 =
=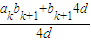 =
=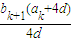 =
=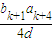 (6分)
(6分)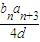 ;(8分)
;(8分)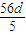 >0,所以d<0
>0,所以d<0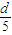 >0,a17=a5+12d=
>0,a17=a5+12d= <0,(11分)
<0,(11分)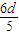 >0,a18=a5+13d=
>0,a18=a5+13d=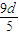 <0,
<0,

 满足:
满足: .
.