
| A�� | ֱ�� | B�� | ��Բ | C�� | ˫���� | D�� | Բ |
���� �������귽�̦�2=$\frac{12}{3co{s}^{2}��+4si{n}^{2}��}$��Ϊ��ͨ���̣����������任$\left\{\begin{array}{l}{x��=\frac{1}{2}x}\\{y��=\frac{\sqrt{3}}{3}y}\end{array}\right.$�����жϣ�
��� �⣺�����귽�̦�2=$\frac{12}{3co{s}^{2}��+4si{n}^{2}��}$��
�ɵã�3y2+4x2=12����$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{4}=1$��
����C���������任$\left\{\begin{array}{l}{x��=\frac{1}{2}x}\\{y��=\frac{\sqrt{3}}{3}y}\end{array}\right.$���ɵ�$\left\{\begin{array}{l}{2x��=x}\\{\sqrt{3}y��=y}\end{array}\right.$����������C�ɵã�$\frac{x{��}^{2}}{\frac{3}{4}}+\frac{y{��}^{2}}{\frac{4}{3}}=1$��
�������任�õ�����������Բ��
��ѡ��B��
���� ������Ҫ�����˼����귽������ͨ���̵Ļ����Լ������任�����������ڻ����⣮


 �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\overrightarrow{a}$=��0��0����$\overrightarrow{b}$=��1��-2�� | B�� | $\overrightarrow{a}$=��-1��2����$\overrightarrow{b}$=��5��7�� | C�� | $\overrightarrow{a}$=��3��5����$\overrightarrow{b}$=��6��10�� | D�� | $\overrightarrow{a}$=��2��-3����$\overrightarrow{b}$=��4��-6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
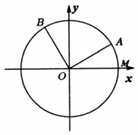 ��ͼ����֪��λԲO��x���������ཻ�ڵ�M����A��B�ڵ�λԲ�ϣ����е�A�ڵ�һ���ޣ��ҡ�AOB=$\frac{��}{2}$���ǡ�MOA=������MOB=�£�
��ͼ����֪��λԲO��x���������ཻ�ڵ�M����A��B�ڵ�λԲ�ϣ����е�A�ڵ�һ���ޣ��ҡ�AOB=$\frac{��}{2}$���ǡ�MOA=������MOB=�£��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
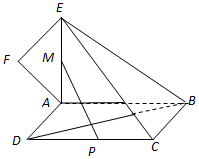 ��ͼ��������ABCD����ƽ�����ı���ABEF����ƽ�滥�ഹֱ����ABE�ǵ���ֱ�������Σ�AB=AE��FA=FE����AEF=45�㣮
��ͼ��������ABCD����ƽ�����ı���ABEF����ƽ�滥�ഹֱ����ABE�ǵ���ֱ�������Σ�AB=AE��FA=FE����AEF=45�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{6}$ | B�� | 3$\sqrt{6}$ | C�� | 2 | D�� | 5$\sqrt{6}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com