
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |

| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
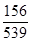 (2) 2×2列联表如下:
(2) 2×2列联表如下:| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | 60 | 40 | 100 |
| 女生 | 70 | 30 | 100 |
| 合计 | 130 | 70 | 200 |
 =
=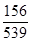 .
.| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | 60 | 40 | 100 |
| 女生 | 70 | 30 | 100 |
| 合计 | 130 | 70 | 200 |
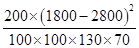 =
=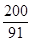 ≈2.20,
≈2.20,

科目:高中数学 来源:不详 题型:解答题
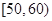 ,
,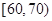 ,
,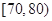 ,
,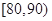 ,
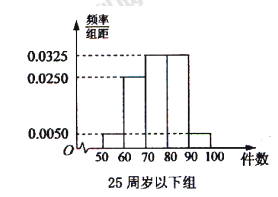
,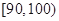 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.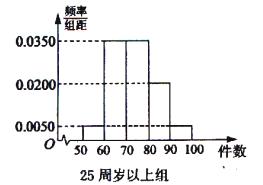

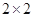 的列联表,并判断是否有
的列联表,并判断是否有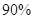 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 分组(体重) |  |  | 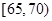 |  |
| 频数(人) |  |  |  |  |
 的频率;
的频率; 中共有几人?
中共有几人? 的人中,任取2人,求体重在
的人中,任取2人,求体重在 中各有1人的概率.
中各有1人的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 名男生和
名男生和 名女生进行了不记名的问卷调查,得到了如下的统计结果:
名女生进行了不记名的问卷调查,得到了如下的统计结果:| 上网时间(分钟) |  |  |  |  |  |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) |  |  |  |  |  |
| 人数 | 10 | 20 | 40 | 20 | 10 |
 列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |
 ,其中
,其中
 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
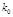 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 年份 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 |
| x(kg) | 70 | 74 | 80 | 78 | 85 | 92 | 90 | 95 |
| y(t) | 5.1 | 6.0 | 6.8 | 7.8 | 9.0 | 10.2 | 10.0 | 12.0 |
| | ||||||||
| 年份 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | |
| x(kg) | 92 | 108 | 115 | 123 | 130 | 138 | 145 | |
| y(t) | 11.5 | 11.0 | 11.8 | 12.2 | 12.5 | 12.8 | 13.0 | |
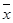 =101,
=101,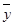 ≈10.113 3,
≈10.113 3,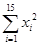 =161 125,
=161 125,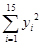 =1 628.55,
=1 628.55,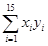 =16 076.8)
=16 076.8)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 之间的几组数据如下表:
之间的几组数据如下表: | 1 | 2 | 3 | 4 | 5 | 6 |
 | 0 | 2 | 1 | 3 | 3 | 4 |

 求得的直线方程为
求得的直线方程为 则以下结论正确的是( )
则以下结论正确的是( ) B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 环数(环) | 8 | 9 |
| 人数(人) | 7 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com