练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某二手交易市场对某型号的二手汽车的使用年数（）与销售价格（单位：万元/辆）进行整理，得到如下的对应数据：

    使用年数

    2

    4

    6

    8

    10

    销售价格

    16

    13

    9.5

    7

    4.5

    （I）试求关于的回归直线方程.

    （参考公式：，）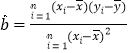

    （II）已知每辆该型号汽车的收购价格为万元，根据（I）中所求的回归方程，预测为何值时，销售一辆该型号汽车所获得的利润最大？（利润=销售价格-收购价格）

    【答案】（I）.

    （II）当时，利润取得最大值.

    【解析】分析：（I）由题意可求得，结合所给公式可得，从而可得线性回归方程．（II）由题意可得，根据二次函数的知识求得最值即可．

    详解：（I）由表中数据得

    ，

    ，

    ，

    ，

    ∴，

    ∴，

    ∴关于的回归直线方程为．

    （II）根据题意得利润

    ∴当时，利润取得最大值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】函数 .

    （1）当时，讨论的单调性；

    （2）若函数有两个极值点，且，证明： .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】按要求写出下列命题，并判断真假：

    （1）命题：“在中，若则”的逆命题；

    （2）命题：“若两个数的和为有理数，则这两个数都是有理数。”的否命题；

    （3）命题：“若a≠0且b≠0,则ab≠0”的逆否命题；

    （4）命题：“a=0或b=0,则a2+b2=0”的逆否命题；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法正确的是（ ）

    A. 天气预报说明天下雨的概率为，则明天一定会下雨

    B. 不可能事件不是确定事件

    C. 统计中用相关系数来衡量两个变量的线性关系的强弱，若则两个变量正相关很强

    D. 某种彩票的中奖率是，则买1000张这种彩票一定能中奖

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C的中心在原点，离心率等于，它的一个短轴端点恰好是抛物线的焦点．

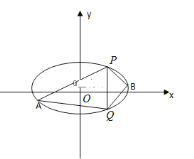
    （1）求椭圆C的方程；

    （2）已知P（2，3）、Q（2，﹣3）是椭圆上的两点，A，B是椭圆上位于直线PQ两侧的动点，若直线AB的斜率为，求四边形APBQ面积的最大值；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直三棱柱中，为等腰直角三角形，，且，分别为，，的中点．

    （1）求证：直线平面；

    （2）求与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学为弘扬优良传统，展示80年来的办学成果，特举办“建校80周年教育成果展示月”活动。现在需要招募活动开幕式的志愿者，在众多候选人中选取100名志愿者，为了在志愿者中选拔出节目主持人，现按身高分组，得到的频率分布表如图所示

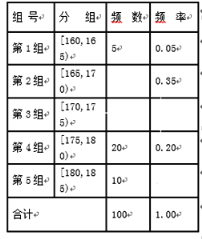
    （1）请补充频率分布表中空白位置相应数据，再在答题纸上完成下列频率分布直方图；

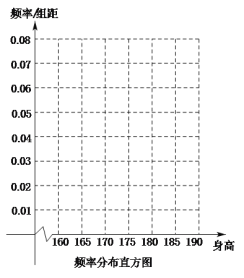
    （2）为选拔出主持人，决定在第3、4、5组中用分层抽样抽取6人上台，求第3、4、5组每组各抽取多少人？

    （3）在（2）的前提下，主持人会在上台的6人中随机抽取2人表演诗歌朗诵，求第3组至少有一人被抽取的概率？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着资本市场的强势进入，互联网共享单车“忽如一夜春风来”，遍布了一二线城市的大街小巷.为了解共享单车在市的使用情况，某调查机构借助网络进行了问卷调查，并从参与调查的网友中随机抽取了200人进行抽样分析，得到下表（单位：人）：

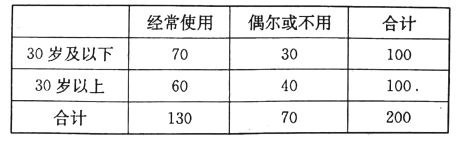
    （Ⅰ）根据以上数据，能否在犯错误的概率不超过0.15的前提下认为市使用共享单车情况与年龄有关？（Ⅱ）①现从所抽取的30岁以上的网民中，按“经常使用”与“偶尔或不用”这两种类型进行分层抽样抽取10人，然后，再从这10人中随机选出3人赠送优惠券，求选出的3人中至少有2人经常使用共享单车的概率.

    ②将频率视为概率，从市所有参与调查的网民中随机抽取10人赠送礼品，记其中经常使用共享单车的人数为，求的数学期望和方差.

    参考公式： ，其中.

    参考数据：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，直线不过原点且不平行于坐标轴，与交于、两点，线段的中点为．

    （1）证明：直线的斜率与的斜率的乘积为定值；

    （2）若过点，延长线段与交于点，四边形能否为平行四边形？若能，求出的方程；若不能，说明理由．

    查看答案和解析>>

    同步练习册答案